题目:在 n×n 方阵里填入 1,2,...n×n, 要求蛇形填数。例如,n=4 时方阵为:
10 11 12 1
9 16 13 2
8 15 14 3
7 6 5 4
空格不严格要求输出,其中(n<=8)。
解:
1 #include <stdio.h> 2 #include <string.h> 3 4 #define maxn 20 5 int a[maxn][maxn]; 6 7 int main () 8 { 9 int n , x , y , tot = 0; 10 scanf("%d",&n); 11 memset(a,0,sizeof(a)); 12 tot = a[x = 0][y = n-1] = 1; 13 14 while (tot < n*n) 15 { 16 while (x+1<n && !a[x+1][y]) a[++x][y] = ++tot; 17 while (y-1>=0 && !a[x][y-1]) a[x][--y] = ++ tot; 18 while (x-1>=0 && !a[x-1][y]) a[--x][y] = ++tot; 19 while (y+1<n && !a[x][y+1]) a[x][++y] = ++tot; 20 21 } 22 23 for (x = 0;x < n;x++) 24 { 25 for (y = 0;y < n;y++) 26 { 27 printf("%3d",a[x][y]); //输出和例题一样的格式 28 } 29 printf("\n"); 30 } 31 32 return 0; 33 }
下面对一些细节进行探究:
一、二维数组的数学抽象
由于我们无法控制鼠标的位置,我们只能通过平面的坐标系来定位每一个数的位置,在顺次输出几个。这就涉及到了平面坐标系在C语言中的抽象,很显然的,我们使用二维数组。
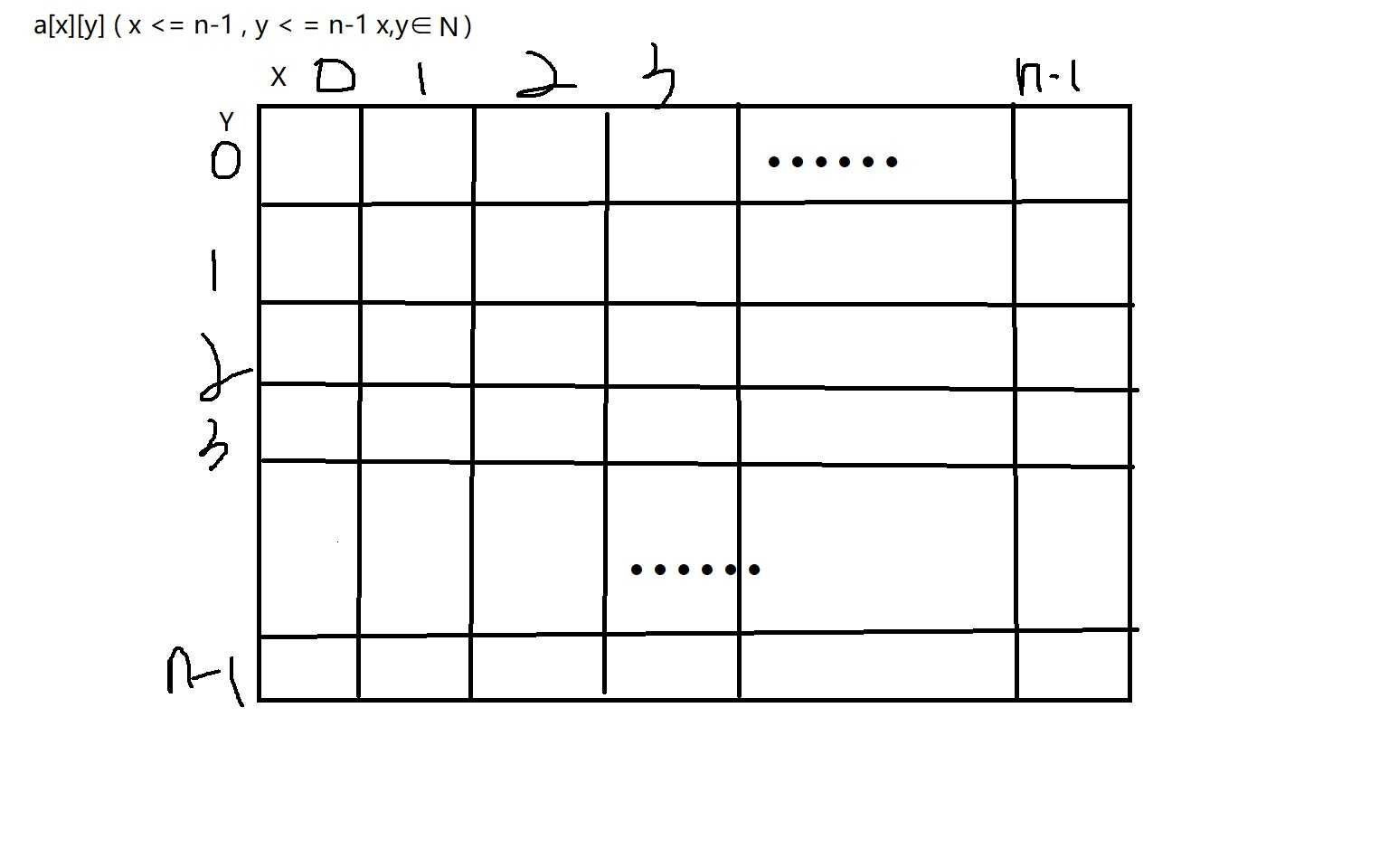
每一个格子就是一个坐标,这样抽象的好处是我们无需考虑其如何输出,只需要考虑我们如何赋值即可。
另外的一个技巧是:将整个数组初始化为0,这样0就代表是该坐标位置未被占去的状态,可以用!a[x][y}是否为1来判断。并且,无论格子内填了什么,!a[x][y]的值都会是0。
二、简化运算符的使用
就像书上说的一样,
tot = a[x = 0][y = n-1] = 1;
这句话包含了很大的信息量。不仅使得代码变得简洁,而且没有使程序的易读性丧失。
三、短路运算符的妙用
当你不能避免某一条语句会导致下标溢出的时候,使用短路运算符可以很好的解决问题。就比如将!a[x+1][y]放入&&的后面,即使x+1>=n也不会使得下标溢出。
四、细节问题
注意观察变量的情况。如果tot的初始值为1,那么下面的句子就要使用tot++。
来自:《算法竞赛入门经典》--紫皮书
原文:https://www.cnblogs.com/nowonder/p/snake-like-fill-in.html