含义:按某条路径巡访树中的每个结点,使得每个节点均被访问一次,且仅被访问一次
目的:它是树结构增、删、改、查以及排序运算的前提,是二叉树一切运算的基础和核心。
遍历规则
二叉树由根、左子树、右子树构成,定义为D、L、R
D、L、R的 组合定义了六种可能的遍历方案:
LDR,LRD,DLR,DRL,RDL,RLD
若限定先左后右,则有三种实现方案:
| DLR | LDR | LRD |
| 先序遍历 | 中序遍历 | 后续遍历 |
注:“先、中、后”的意思是指访问的结点D是先于子树出现还是后于子树出现。
先序遍历
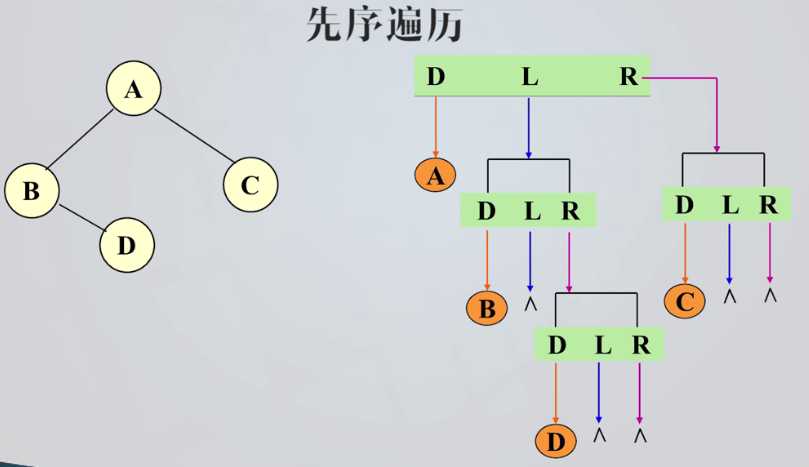
先序遍历序列:A B D C
任意一个结点均处在其子女结点的前面(根结点在前)
中序遍历
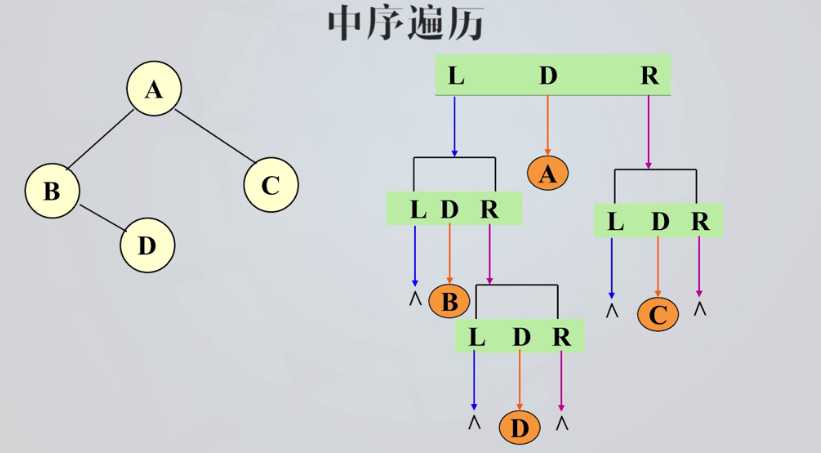
中序遍历序列:B D A C
根结点左右分别为左右子树的所有结点。
后序遍历
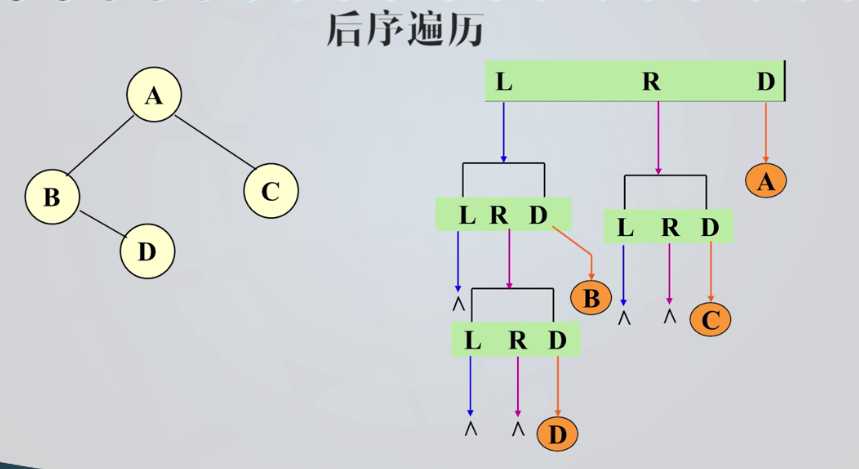
后序遍历序列:D B C A
结点数据类型自定义
typedef struct node{
int data;
struct node *lchild,*rchild;
}node;
node *root;
先序遍历算法
status PreOrderTraversal(BiTree T)
{if (T) //非空二叉树
{visit(T->data); //访问D
PreOrderTraversal(T->lchild); //递归遍历左子树
PreOrderTraversal(T->rchild); //递归遍历右子树
}
return OK; }
中序遍历算法
status InOrderTraversal(BiTree T)
{if (T) //非空二叉树
{
InOrderTraversal(T->lchild); //递归遍历左子树
visit(T->data); //访问D
InOrderTraversal(T->rchild); //递归遍历右子树
}
return OK; }
后序遍历算法
status PostOrderTraversal(BiTree T)
{if (T) //非空二叉树
{
PostOrderTraversal(T->lchild); //递归遍历左子树
PostOrderTraversal(T->rchild); //递归遍历右子树
visit(T->data); //访问D
}
return OK; }
遍历的分析
从前面的三种遍历算法可以知道:如果将visit语句抹去,从递归的角度看,这三种算法是完全相同的,或者说这三种遍历算法的访问路径是相同的,只是访问结点的时机不同。
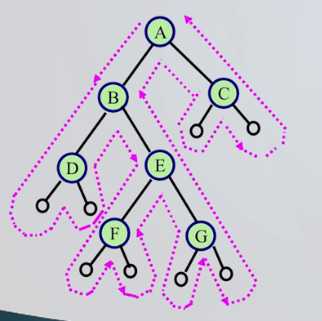
从虚线的出发点到终点的路径上,每个结点经过3次。
第1次经过时访问,是先序遍历。
第2次经过时访问,是中序遍历。
第3次经过时访问,是后序遍历。
二叉树遍历的时间效率和空间效率
时间效率:O(n)//每个结点只访问一次
空间效率:O(n) //栈占用的最大辅助空间
遇到结点就把它入栈,然后遍历它的左子树。
当左子树遍历结束,从栈顶弹出该结点并访问它。
以右指针再去中序遍历右子树。
Status InOrderTraverse(BiTree T,Status(*Visit)(TElemType e)){
InitStack(S); p=T;
while (p || !StackEmpt(s)){
if(p) {Push(S,p); p=p->lchild;} //根指针进栈,遍历左子树 //调换位置,可以更改为先序遍历
else{
Pop(S,p);
if(! Visit(p->data)) return ERROR;
p=p->rchild; //调换位置,可以更改为先序遍历
}//else
}//while
return OK;
}
}
二叉树的遍历
二叉树的遍历就是按某条路径巡访树中每个结点,使得每个节点均被访问一次,且仅被访问一次。
层序遍历
从上之下,从左到右,顺序访问
队列数据结构:先进先出 根-左-右
队列实现:
1、根结点入队;
2、执行下列循环:结点出队,访问该结点,其左、右儿子入队;
3、队列为空时,结束。
层序遍历的算法过程为:
1、根结点入队;
2、从队列中取出一个元素,即访问该元素;
3、若该元素结点的左、右孩子非空,则将其左、右孩子结点元素顺序入队;
4、循环执行2,3步,直到队列为空,结束。
void LevelOrderTraversal(BinTreeBT){
Queue Q; BinTree T;
if(!BT) return; //若是空树则直接返回
Q = CreatQueue(MaxSize); //创建并初始化队列
AddQ(Q,BT);
T = DeleteQ(Q);
printf(“%d\n”,T->Data); //访问取出队列的结点
if (T->Left)AddQ(Q,T->left);
if(T->Right)AddQ(Q,T->Right);
}
统计二叉树中叶子结点的个数(先序遍历)
算法思想:
利用先序(或中序或后序)遍历二叉树,在遍历过程中查找叶子结点,并进行计数。
在遍历算法中增加一个“计数”的参数;
将遍历算法中“访问结点的操作”改为:若是叶子结点,则计数器加1.
status PreOrderTraversal(BiTree T)
{if (T) //非空二叉树
{if(!T->lchild)&&(!T->rchild)
count++; //对叶子结点计数 printf(‘’%d‘’,T->data)
PreOrderTraversal(T->lchild); //递归遍历左子树
PreOrderTraversal(T->rchild); //递归遍历右子树
}
return OK; }
求二叉树的深度
算法思想:
首先,分析二叉树的深度和它的左、右子树深度之间的关系
二叉树的深度应该为其左、右子树深度的最大值加1.
由此,可以先分别求得左、右子树的深度。
后序遍历
int PostOrderTraversal(BiTree BT)
{ int HL ,HR,MaxH;
if (BT) //非空二叉树{
HL=PostOrderGetHeight(BT->left); //左子树深度
HR=PostOrderGetHeight(BT->right); //右子树深度
MaxH=(HL >HR) ? HL:HR; //取左右子树较大的深度
return (MaxH +1) //返回树的深度
}
else return 0; //空树返回0
}
已知三种遍历中的任意两种序列,能否唯一确定一棵二叉树呢?
答案是:必须要有中序遍历才行!
没有中序的困扰:
先序遍历序列:AB
后序遍历序列:BA
A A
↙ ↘
B B
不能确定左右子树的边界
由二叉树的先序和中序来确定二叉树
由先序遍历序列,确定第一个结点元素为根结点;
根据根结点在中序序列中的位置,分割出左右子树的子序列;
对左子树和右子树再分别递归使用相同的方法继续分析。
先序序列:根 左子树 右子树
中序序列:左子树 根 右子树
例:
先序序列:a bcde fghij
中序序列:cbed a ghijf
原文:https://www.cnblogs.com/privilege/p/11218220.html