287. 寻找重复数

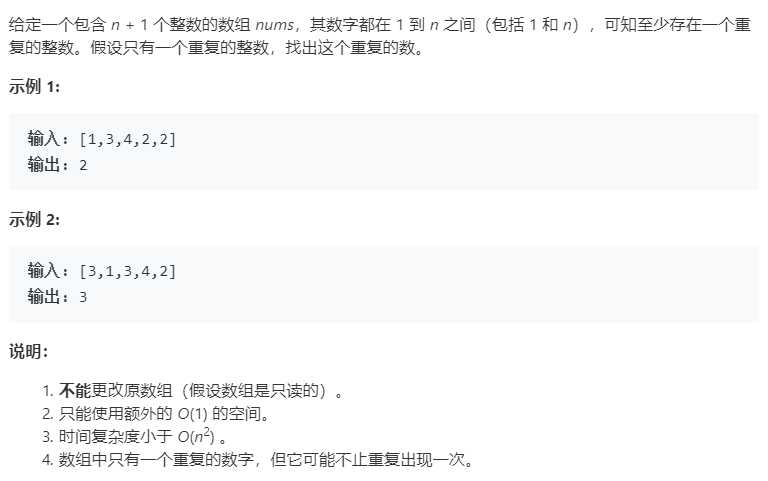
这题的难点就在于下面的说明了，我们先不管下面的那些说明的要求，用常规的解法来解答下上的题目。

排序思想解法

先把原来的数组进行排序，然后逐个遍历，一旦发现后一个元素和当前的元素相等，那么就返回，这就是我们找到了重复数字。但是这种思想，就不满足说明里面的，不能改变原数组，虽然时间复杂度是满足O（n^2）。

哈希思想

用个哈希集合（HashSet）来记录已经出现过的元素，一旦遍历到了元素曾经出现在集合当中，那么就返回，这就是需要寻找的重复数字。

重新排序的思想

这种思想说起来有点复杂，但是时间复杂度是最好的。
我们从头开始遍历数组，遍历到的下标为i，那么我们就分两种情况来讨论：

1. 如果num[i]等于(i+1)，就是值等于刚好等于下标那么就遍历到下一个。因为刚刚好这个就是对应的，我们就不管他了。

2. 如果num[i]和(i+1)不等，那么就去吧下标等于（num[i] - 1）的数字和这个数字进行交换（下标为i），这样再去判断如今的这个位置上的value和index是否相等，如果不等，继续交换。交换到这个位置上的num[i]和(i+1)相等为止；或者你会找到一个数字，这个数字，那个数字在对应的位置上已经有了，那么这个就是重复的那个数字了。

   Talk is cheap, show me the code.

public int findDuplicate(int[] nums) {
    if (nums.length == 0) {
        return 0;
    }
    int res = 0;
    for (int i = 0, len = nums.length; i < len; i++) {
        int temp = i + 1;
//          判断num[i]的值是不是就是放在这
        if (temp == nums[i]) {
            continue;
        } else {
//              两个不相同就进入循环，
            while (temp != nums [i]) {
                int newIndex = nums[i] - 1;
//                  如果位置上的数字和num[i]相等，那么就表示出现重复的数字，
                if (nums[newIndex] == nums[i]) {
                    return nums[i];
                }
//                    交换两个元素
                int swapTemp = nums[newIndex];
                nums[newIndex] = nums[i];
                nums[i] = swapTemp;
            }
        }
    }
    return res;
}

当然了，以上依然不是最好的解法。因为虽然时间是O（n），但是却把原来的数组变动了。

用二分思想

这里的思想有点复杂，大概的思想是这样：
我们先假设一个如果排序好的数组中，你如果取中间的数字，那么如果你的这个中间数 是要比当前的索引的坐标大的话，那么就是也就是nums[i] > i，那么就是说明那个重复的数字是在后半部分的，因为只有在后半部分有重复数字存在的时候，才会多出一个数字来，那么我们就用二分法，吧start取到中点位置，继续寻找；反之，那个重复的数字是在前半部的。
因为我们这数组是没排序的数组，那么我们根据上面的那个计数的思想，我们先取一个取值范围，如果数组里面的元素的取值在这个取值范围的元素个数，等于这个取值范围的区间，那么就表示这个取值范围内不存在重复元素，我们要取别的区间的，继续计数。

public int findDuplicateNew(int[] nums) {
    int start = 1;
    int end = nums.length;
    while (start <= end) {
//            取中值
        int middle = start + ((end - start) >> 1);
//            计算从开始值到中值区间内有多少数字。
        int tempCount = countRange(nums, start, middle);
//            如果已经区间已经缩小的到了只有一个数了，那么就可以判断在区间内的数字是不是有两个了。
        if (start == end) {
            if (tempCount > 1) {
                return start;
            } else {
                break;
            }
        }

//            区间就是 中值- 开始值 + 1。然后开始和计数比较。
        int range = middle - start + 1;
        if (tempCount > range) {
            end = middle;
        } else if (tempCount <= range) {
            start = middle + 1;
        }
    }
    return -1;
}

//    计数比较，时间复杂度为O(n)
private int countRange(int[] nums, int start, int end) {
    int count = 0;
    for (int item : nums) {
        if (item >= start && item <= end ) {
            count++;
        }
    }
    return count;
}

以上的时间复杂度是$O(NlogN)$ ，二分的时间复杂度是$O(logN)$，每次计数的时间复杂度是$O(N)$。

287. 寻找重复数 Java解法

原文：https://www.cnblogs.com/jamesmarva/p/11210000.html