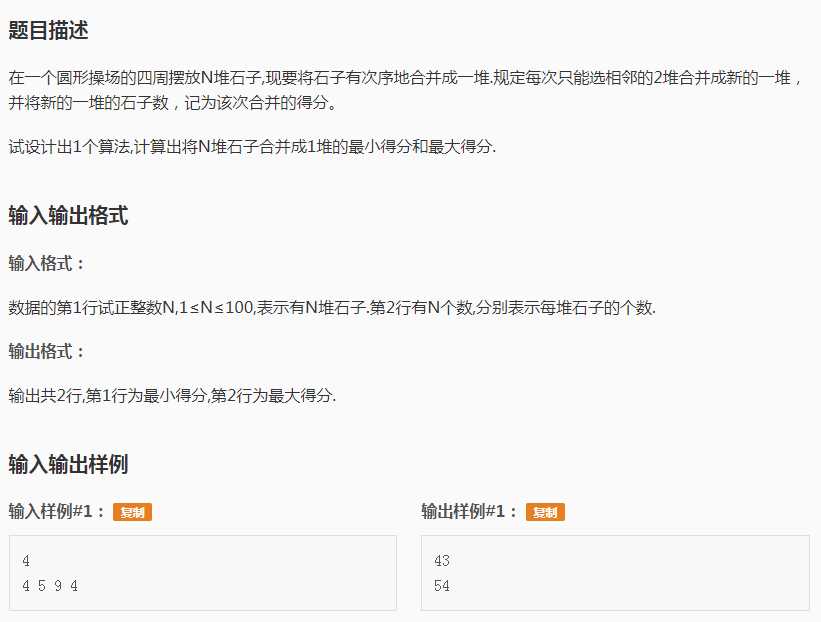
环状区间DP板子题
#include<stdio.h> #include<stdlib.h> #include<string.h> #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) using namespace std; const int N=100; int n,min_ans=214748364,max_ans,a[N+1],s[N+1],f1[N+1][N+1],f2[N+1][N+1];//f1[i][j]为i-j这区间合并在一起的最小值,f2[i][j]为i-j这区间合并在一起的最大值 inline int min(int a,int b){return a<b?a:b;} inline int max(int a,int b){return a>b?a:b;} int main() { scanf("%d",&n); FORa(i,1,n) scanf("%d",&a[i]); FORa(k,1,n) { int p=a[1]; FORa(i,1,n) a[i-1]=a[i];//将链进行更新操作 a[n]=p,s[0]=0; FORa(i,1,n) s[i]=s[i-1]+a[i];//s[]为前缀和数组,优化常数 memset(f1,127/3,sizeof(f1)); memset(f2,0,sizeof(f2));//每一次都需要赋初值 FORa(i,1,n) f1[i][i]=0;//初状态的确定 FORs(i,n-1,1) FORa(j,i+1,n) FORa(k,i,j-1) f1[i][j]=min(f1[i][j],f1[i][k]+f1[k+1][j]+s[j]-s[i-1]),f2[i][j]=max(f2[i][j],f2[i][k]+f2[k+1][j]+s[j]-s[i-1]); //状态转移方程 min_ans=min(min_ans,f1[1][n]),max_ans=max(max_ans,f2[1][n]);//筛选答案 } printf("%d\n%d",min_ans,max_ans); return 0; }
#include<stdio.h> #include<stdlib.h> #include<string.h> #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) using namespace std; const int N=100; int n,min_ans=214748364,max_ans,a[2*N+2],s[2*N+2],f1[2*N+2][2*N+2],f2[2*N+2][2*N+2];//f1[i][j]为i-j这区间合并在一起的最小值,f2[i][j]为i-j这区间合并在一起的最大值 inline int min(int a,int b){return a<b?a:b;} inline int max(int a,int b){return a>b?a:b;} int main() { scanf("%d",&n); FORa(i,1,n) scanf("%d",&a[i]),a[i+n]=a[i],s[i]=s[i-1]+a[i];//化环为链, FORa(i,n+1,2*n) s[i]=s[i-1]+a[i];//s[]为前缀和数组,优化常数 memset(f1,127/3,sizeof(f1)); FORa(i,1,2*n) f1[i][i]=0; FORs(i,2*n-1,1) for(int j=i+1;j<=2*n&&j-i<=n;j++) FORa(k,i,j-1) f1[i][j]=min(f1[i][j],f1[i][k]+f1[k+1][j]+s[j]-s[i-1]),f2[i][j]=max(f2[i][j],f2[i][k]+f2[k+1][j]+s[j]-s[i-1]);//状态转移方程 FORa(i,1,n) min_ans=min(min_ans,f1[i][i+n-1]),max_ans=max(max_ans,f2[i][i+n-1]);//筛选答案 printf("%d\n%d",min_ans,max_ans); return 0; }
化繁为简,确定DP本身的性质
原文:https://www.cnblogs.com/SeanOcean/p/11208890.html