感觉我整理数据结构的速度永远跟不上考试的速度啊…
那么!撰写日期是在7.17,在这一天的模拟赛的T2用到了线段树。虽然打出来了板子但是忘掉了一些东西。
就趁着这个机会AK线段树吧!!
线段树是基于分治思想的二叉树结构。树上的每一个节点都代表一个区间,其根节点就是整个统计范围(1-N),每一个叶节点就是长度为1的区间(也就是一个元素)。对于每个内部节点[l-r],它的左节点是[l,mid],右节点是[mid+1,r],其中mid=(l+r)/2(向下取整)。
根据这些定义,我们大概也能判断他常用的题型了。什么区间最值啊之类的涉及区间的东西。因为他大多情况下是一颗比较完整的完全二叉树(我的意思是不会浪费特别大的空间…),所以我们一般用“父子二倍”的编号方法。即根节点编号为1。对于任意一个节点x,它的左节点为2x,右节点为2x+1。为了保证不会越界,对于N个叶节点的线段树,我们将数组的长度开到4N
线段树的基本用途就是对序列的维护,支持查询与修改指令。线段树可以非常方便的从下向上传递信息。我们举个区间最小值的例子(诶嘿就是要跟小蓝书反着走!),对于一个节点Data(l,r),显然Data(l,r)=min(Data(l,mid),Data(mid+1,r))。所以啊,我们用一个结构体保存每个节点。每个节点就包括三个信息。区间左端点L,区间右端点R,和这个节点存放的值Data
那么接下来上一手区间最小值的代码233
struct S{ int l,r; int dat; }T[4*MAXN]; void build(int p,int l,int r){ T[p].l=l;//别问我P是什么东西,你用数组的时候总要有个下标的吧= = T[p].r=r; if(l==r){//叶子节点!! T[p].dat=R[l]; return; } int mid=(T[p].l+T[p].r)/2; build(p*2,l,mid);//左节点 build(p*2+1,mid+1,r);//右节点 T[p].dat=min(T[p*2].dat,T[p*2+1].dat);//如果你想改成区间最大值,就把这个min函数改动一下好了。 } build(1,1,n);//入口
这里支持的修改是单点,也就是一次只更改一个节点的值。你可以指定他改成某个元素或者令他进行计算以改变值。
在线段树中,根节点是各种指令的入口。我们需要从根节点出发,层层递归来找代表着所需区间的节点。然后从下往上更新。
下面上的是复杂度为O(log N)的单点修改
void change(int p,int x,int v){ //v是要减小的值,p是入口,x是所需更该节点的位置 if(T[p].l==T[p].r){ T[p].dat-=v; return; } int mid=(T[p].l+T[p].r)/2; if(x<=mid){ change(p*2,x,v); } else{ change(p*2+1,x,v); } T[p].dat=min(T[p*2].dat,T[p*2+1].dat); } change(1,x,v);//入口
注意:为了把功能放在一起,所以我把这个知识点放在了单点修改下面。但这个知识点更接近于压轴难度。所以可以先看下面的查询功能,再来看这个区间修改。
(小声)怎么办小蓝书上并没有纯粹的区间修改…给了个例题还加持了数论的buff
啊数论啊!我数学蒟蒻啊兄Dei!!

好的我们换一个质朴的例题来打板子吧。
(说着他翻开了小蓝书的下一页,并发现了藏在延迟标记里的区间修改)
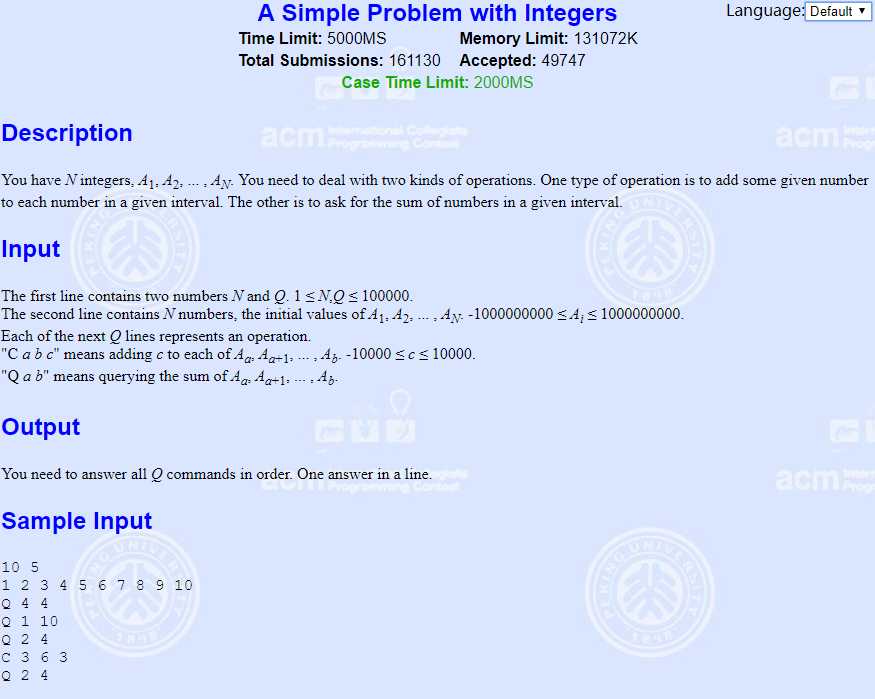

如果我们要修改区间,那么想想看,如何实现?
众所周知,OI的本质就是倒水(雾)。我们最轻松可以想到的是,直接循环调用单点修改。
那么我们本来高效的O(log N)就这么变成了O(N)!!!!这不能忍。可怎么想,这也没什么可优化的余地啊。那怎么办?
偷懒啊!
什么意思?我们仔细思考一下,这就和我们做作业是一个道理。最恐怖的不是你没做作业,最恐怖的是你废了一大堆时间做作业,老!师!不!检!查!(大雾!!!)
所以,我们就在他每次要求我们修改的时候,只要他不问,我就不修改!
那我怎么要在他问的时候还能让程序记着这个点要修改了再用呢?
这就是延迟标记(也有人叫懒惰/Lazy标记)的作用咯。
那也就是说,我们要在执行修改指令时,发现P点所在区间被完全覆盖时,可以立即返回,不过我们要留一个延迟标记再走。
在后续的指令中,往下递归的时候,如果发现了这里存在一个延迟标记,那么就根据这个标记的内容来更新下方的节点,同时清除这个标记,为下方的子节点打上标记。
故,这个标记的真正定义是:
这个节点曾经被修改,但其子节点尚未被更新。
请留意这个概念,因为犯错概率有点大…
下面放出代码,有些长。
#include<iostream> using namespace std; const int MAXN=100010; struct SegmentTree{ int l,r; long long sum,add;//这个add就是所谓的延迟标记! }tree[MAXN*4]; int a[MAXN],n,m; void build(int p,int l,int r){ tree[p].l=l; tree[p].r=r; if(l==r){ tree[p].sum=a[l]; return ; } int mid=(l+r)/2; build(p*2,l,mid); build(p*2+1,mid+1,r); tree[p].sum=tree[p*2].sum+tree[p*2+1].sum; } void spread(int p){ if(tree[p].add){ //如果这个节点被标记了延迟标记 /* ----------Warning-------- 延迟标记的意义,是“这个节点曾经被修改,但其子节点尚未被更新。”也就是说,他自己已经更新过了 但他下面的子节点都没有更新。这就意味着我们遇到这个标记的时候,要对他的子节点进行更新。 */ tree[p*2].sum+=tree[p].add*(tree[p*2].r-tree[p*2].l+1);//更新左节点 tree[p*2+1].sum+=tree[p].add*(tree[p*2+1].r-tree[p*2+1].l+1);//更新右节点 tree[p*2].add+=tree[p].add;//给左节点打标 tree[p*2+1].add+=tree[p].add;//给右节点打标 tree[p].add=0;//清除p的标记 } } void change(int p,int l,int r,int d){ if(l<=tree[p].l&&r>=tree[p].r){ tree[p].sum+=(long long)d*(tree[p].r-tree[p].l+1);//更新该节点 tree[p].add+=d;//打上延迟标记 return ; } spread(p);//传播延迟标记 int mid=(tree[p].l+tree[p].r)/2; if(l<=mid){ change(p*2,l,r,d); } if(l>mid){ change(p*2+1,l,r,d); } tree[p].sum=tree[p*2].sum+tree[p*2+1].sum; } long long ask(int p,int l,int r){ if(l<=tree[p].l&&r>=tree[p].r){ return tree[p].sum; } spread(p); int mid=(tree[p].l+tree[p].r)/2; long long val=0; if(l<=mid){ val+=ask(p*2,l,r); } if(r>mid){ val+=ask(p*2+1,l,r); } return val; } int main(){ cin>>n>>m; for(int i=1;i<=n;i++){ cin>>a[i]; } build(1,1,n); while(m--){ char op[2];int l,r,d; cin>>op>>l>>r; if(op[0]==‘C‘){ cin>>d; change(1,l,r,d); } else{ cout<<ask(1,l,r)<<endl; } } }
想查询某个区间的最值等等?就在这个功能里实现啦!
我们只需要从根节点开始,递归执行这样的操作:
//注:下面的l,r代表的是你需要查询的区间左端点、右端点。
1.若[l,r]完全覆盖了当前节点代表的区间,那么立即回溯,并将该节点的Data值作为候选答案
2.若左子节点和[l,r]有重叠部分,则递归访问左子节点
3.若右子节点与[l,r]有重叠,则递归访问右子节点
那么附上查询的代码
int ask(int p,int l,int r){ if(l<=T[p].l&&r>=T[p].r){ return T[p].dat; } int mid=(T[p].l+T[p].r)/2; int val=1<<30;//如果你要查询区间最大值,那么把这个值加个负号就好了。 if(l<=mid){ val=min(val,ask(p*2,l,r)); } if(r>mid){ val=min(val,ask(p*2+1,l,r)); } return val; }
原文:https://www.cnblogs.com/Uninstalllingyi/p/11201045.html