q次操作
1.将第l~r个数的左边和和右边都加上一个数d， 使得这个数变成 dsiddsid的形式
2.询问区间和.
题解:对于一个数字x若执行第一个操作则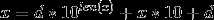 
则若对于一个区间sum(l,r)执行第一个操作则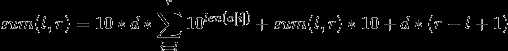 
设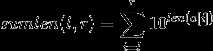 
则便可以用线段树去维护这两个东西便可,这里只考虑了d是一位数的情况,但是在线段树下传标记的过程中可能一个区间多次执行第一个操作,那么wrap的d便不是一位数,而且左右两边的d是镜像的,我们便要用两个lazy标记,lazy1维护左边加的数,lazy2维护右边加的数,同时可以用lazylen表示这两个lazy的,然后好好考虑一下如何维护sum和sumlen即可
个人感悟：在敲的时候思路是基本对的 ， 但是我在维护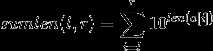 的时候 为了计算10的多少次幂,我维护的是一个长度 ，然后查询的时候，用一个阶乘的fac10[]数组 ， 果然RE了 ， 大神的代码， 发现别人维护的是一个10^（len）的值，其实细想也是，我们主要维护的就是这个，我居然多次了一举，太菜了我
#include <iostream> #include <string.h> #include <algorithm> #include <stdio.h> #include <math.h> #include <queue> #define MAXN 400010 #define inf 0x3f3f3f3f #define LL long long using namespace std; const int N=1e7+5; const int mod = 1e9+7; struct node{ int l,r; //区间[l,r] LL addl,addr; //区间的延时标记 LL sum,laz,all; /// 区间和 laz增加位数 all=10^位数 }tree[MAXN<<2];//一定要开到4倍多的空间 void pushup(int index) { tree[index].sum = (tree[index<<1].sum+tree[index<<1|1].sum)%mod; tree[index].all = (tree[index<<1].all+tree[index<<1|1].all)%mod; } void pushdown(int index) { if(tree[index].laz > 1) { tree[index<<1].addl = (tree[index].addl*tree[index<<1].laz%mod + tree[index<<1].addl%mod)%mod; tree[index<<1|1].addl = (tree[index].addl*tree[index<<1|1].laz%mod + tree[index<<1|1].addl%mod)%mod; tree[index<<1].addr = (tree[index<<1].addr*tree[index].laz%mod + tree[index].addr%mod)%mod; tree[index<<1|1].addr = (tree[index<<1|1].addr*tree[index].laz%mod+ tree[index].addr)%mod; tree[index<<1].sum = (( tree[index<<1].sum*tree[index].laz%mod + tree[index].addl*tree[index<<1].all%mod*tree[index].laz%mod)%mod + tree[index].addr*(tree[index<<1].r-tree[index<<1].l+1)%mod)%mod; tree[index<<1|1].sum = ((tree[index<<1|1].sum*tree[index].laz%mod + tree[index].addl*tree[index<<1|1].all%mod*tree[index].laz%mod)%mod + tree[index].addr*(tree[index<<1|1].r-tree[index<<1|1].l+1)%mod)%mod; tree[index<<1].all = (tree[index<<1].all*tree[index].laz%mod*tree[index].laz)%mod; tree[index<<1|1].all = (tree[index<<1|1].all*tree[index].laz%mod*tree[index].laz)%mod; tree[index<<1].laz = tree[index].laz*tree[index<<1].laz%mod; tree[index<<1|1].laz = tree[index].laz*tree[index<<1|1].laz%mod; tree[index].laz = 1; tree[index].addl = 0; tree[index].addr = 0; } } void build(int l,int r,int index){ tree[index].sum = 0; tree[index].l = l; tree[index].r = r; tree[index].addl = tree[index].addr = 0; tree[index].laz = 1;//刚开始一定要清0 if(l == r) { tree[index].all = 1; return ; } int mid = (l+r)>>1; build(l,mid,index<<1); build(mid+1,r,index<<1|1); pushup(index); } void update(int l,int r,int index,LL val) { if(l <= tree[index].l && r >= tree[index].r) { tree[index].sum = ((tree[index].sum*10%mod + val*(tree[index].r-tree[index].l+1)%mod)%mod + val*10*tree[index].all %mod )%mod ; tree[index].all = tree[index].all*100%mod; tree[index].addl = (val*tree[index].laz%mod + tree[index].addl)%mod; tree[index].laz = tree[index].laz*10%mod; tree[index].addr = (tree[index].addr*10%mod + val)%mod; return ; } pushdown(index); int mid = (tree[index].l+tree[index].r)>>1; if(l <= mid) update(l,r,index<<1,val); if(r > mid) update(l,r,index<<1|1,val); pushup(index); } LL query(int l,int r,int index) { if(l <= tree[index].l && r >= tree[index].r) { return tree[index].sum; } pushdown(index); int mid = (tree[index].l+tree[index].r)>>1; LL ans = 0; if(l <= mid) ans = (ans+query(l,r,index<<1))%mod; if(r > mid) ans = (ans+query(l,r,index<<1|1))%mod; return ans; } int main() { int _; scanf("%d",&_); for(int ncase=1;ncase<=_;ncase++) { int n,m; scanf("%d%d",&n,&m); printf("Case %d:\n",ncase); build(1,n,1); while(m--) { char s[10]; scanf("%s",s); int l,r,v; scanf("%d%d",&l,&r); if(s[0]==‘w‘) { scanf("%d",&v); update(l,r,1,v); } else { printf("%lld\n",query(l,r,1)); } } } return 0; }
2018 CCPC 吉林站 H Lovers || HDU 6562 (线段树哦)
原文：https://www.cnblogs.com/shuaihui520/p/11200227.html
