[BZOJ 4771]七彩树(可持久化线段树+树上差分)

[BZOJ 4771]七彩树(可持久化线段树+树上差分)

题面

给定一棵n个点的有根树，编号依次为1到n，其中1号点是根节点。每个节点都被染上了某一种颜色，其中第i个节点的颜色为c[i]。如果c[i]=c[j]，那么我们认为点i和点j拥有相同的颜色。定义depth[i]为i节点与根节点的距离。为了方便起见，你可以认为树上相邻的两个点之间的距离为1。站在这棵色彩斑斓的树前面，你将面临m个问题。

每个问题包含两个整数x和d，表示询问x子树里且depth不超过depth[x]+d的所有点中出现了多少种本质不同的颜色。请写一个程序，快速回答这些询问。

分析

先不考虑深度限制，我们考虑如何统计颜色。

我们把每种颜色开一个set，set里存储该颜色节点的dfs序。对于一对相同颜色的节点u,v，他们会对u到v的路径上的节点，和lca(u,v)到根节点路径上的节点的答案产生1的贡献。可以用树上差分算法。开一棵线段树，线段树第x个叶子节点存储节点dfs序（记作dfn) 为x的差分值，维护区间和。那么我们把dfn[u]+1,dfn[v]+1,dfn[lca(u,v)]-1即可。查询x子树的时候直接区间查询x的dfs序对应的区间。

那么我们加入一个新节点x的时候如何更新答案呢。这实际上是在处理树链的并。我们在set中找出x的前驱pre和后继nex（按照dfn排序后），dfn[x]+1,dfn[lca(pre,x)]-1,相当于把x到lca(pre,x)的路径加入答案。同理对nex进行操作。注意lca(pre,nex)往上的路径被减了两次，所以dfn[lca(pre,nex)] -1.这里画个图可以方便理解

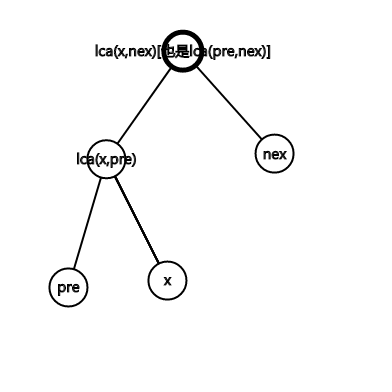
那么有深度限制要怎么做呢？维护可持久化线段树，第i棵可持久化线段树存储深度<=i的树的答案，把节点按深度排序。依次加入对应深度的可持久化线段树。查询的时候直接在对应的线段树中查询x子树即可。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<set>
#define maxn 400000
#define maxlogn 32
using namespace std;
inline int qread(int &x){
    x=0;
    int sign=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-') sign=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=x*10+c-'0';
        c=getchar();
    }
    return x*sign;
}
inline void qprint(int x){
    if(x<0){
        putchar('-');
        qprint(-x);
    }else if(x==0){
        putchar('0');
        return;
    }else{
        if(x/10>0) qprint(x/10);
        putchar('0'+x%10);
    }
}
int t,n,m;
int c[maxn+5];
struct edge{
    int from;
    int to;
    int next;
}E[maxn*2+5];
int sz=1;
int head[maxn+5];
void add_edge(int u,int v){
    sz++;
    E[sz].from=u;
    E[sz].to=v;
    E[sz].next=head[u];
    head[u]=sz;
}

int log2n;
int tim;
int anc[maxn+5][maxlogn+5];
int hash_dfn[maxn+5];
int deep[maxn+5];
int lb[maxn+5],rb[maxn+5];
int id[maxn+5];
int cmp(int x,int y){
    return deep[x]<deep[y];
}

void dfs(int x,int fa){
    tim++;
    lb[x]=tim;
    deep[x]=deep[fa]+1;
    anc[x][0]=fa;
    hash_dfn[lb[x]]=x;
    for(int i=1;i<=log2n;i++) anc[x][i]=anc[anc[x][i-1]][i-1];
    for(int i=head[x];i;i=E[i].next){
        int y=E[i].to;
        if(y!=fa){
            dfs(y,x);
        }
    }
    rb[x]=tim;
}

int lca(int x,int y){
    if(deep[x]<deep[y]) swap(x,y);
    for(int i=log2n;i>=0;i--){
        if(deep[anc[x][i]]>=deep[y]){
            x=anc[x][i];
        }
    }
    if(x==y) return x;
    for(int i=log2n;i>=0;i--){
        if(anc[x][i]!=anc[y][i]){
            x=anc[x][i];
            y=anc[y][i];
        }
    }
    return anc[x][0];
}
struct per_segment_tree{
    //第i棵可持久化线段树维护deep<=i,且dfn在[l,r]内的节点的不同颜色个数 
    struct node{
        int ls;
        int rs;
        int cnt;
    }tree[maxn*maxlogn+5];
    int root[maxn+5];
    int ptr;
    void push_up(int x){
        tree[x].cnt=tree[tree[x].ls].cnt+tree[tree[x].rs].cnt;
    }
    void insert(int &x,int last,int upos,int uval,int l,int r){
        x=++ptr;
        tree[x]=tree[last];
        if(l==r){
            tree[x].cnt+=uval;
            return;
        }
        int mid=(l+r)>>1;
        if(upos<=mid) insert(tree[x].ls,tree[last].ls,upos,uval,l,mid);
        else insert(tree[x].rs,tree[last].rs,upos,uval,mid+1,r);
        push_up(x); 
    }
    int query(int x,int L,int R,int l,int r){
        if(x==0) return tree[x].cnt;
        if(L<=l&&R>=r){
            return tree[x].cnt;
        }
        int mid=(l+r)>>1;
        int ans=0;
        if(L<=mid) ans+=query(tree[x].ls,L,R,l,mid);
        if(R>mid) ans+=query(tree[x].rs,L,R,mid+1,r);
        return ans;
    }
}T;

set<int>s[maxn+5];
void ini(){
    log2n=log2(n)+1;
    tim=0;
    sz=1;
    T.ptr=0;
    for(int i=1;i<=n;i++){//不要memset,会TLE
        anc[i][0]=0;
        c[i]=0;
        deep[i]=0;
        hash_dfn[i]=0;
        head[i]=0;
        id[i]=0;
        lb[i]=0;
        rb[i]=0;
        s[i].clear();
        T.root[i]=0;
    }
}
int main(){

    int u,v;
    qread(t);
    while(t--){
        
        qread(n);
        qread(m);
        ini();
        
        for(int i=1;i<=n;i++) qread(c[i]);
        for(int i=2;i<=n;i++){
            qread(u);
            add_edge(u,i);
            add_edge(i,u);
        }
        dfs(1,0);
        for(int i=1;i<=n;i++) id[i]=i;
        sort(id+1,id+1+n,cmp);
        for(int i=1;i<=n;i++){
            int x=id[i];
            int pre=0,nex=0;

            T.insert(T.root[deep[x]],T.root[deep[id[i-1]]],lb[x],1,1,n);
            set<int>::iterator it=s[c[x]].lower_bound(lb[x]);
            if(it!=s[c[x]].begin()){
                set<int>::iterator it2=it;//不能直接--it,会影响下一个判断 
                pre=hash_dfn[*(--it2)];

                T.insert(T.root[deep[x]],T.root[deep[x]],lb[lca(pre,x)],-1,1,n);
                //x会对pre到x的路径上的点产生1的贡献，树上差分 
                //线段树里的每个店储存的都是差分值 
            }
            if(it!=s[c[x]].end()){
                nex=hash_dfn[*it];

                T.insert(T.root[deep[x]],T.root[deep[x]],lb[lca(x,nex)],-1,1,n);
            }
            //lca(pre,nex)上方的路径被多减了一次，加回来
            if(pre!=0&&nex!=0){

                T.insert(T.root[deep[x]],T.root[deep[x]],lb[lca(pre,nex)],1,1,n);
            } 
            s[c[x]].insert(lb[x]);
        }
        
        int last=0;
        int x,d;
        for(int i=1;i<=m;i++){
            qread(x);
            qread(d);
            x^=last;
            d^=last;
            last=T.query(T.root[min(deep[x]+d,deep[id[n]])],lb[x],rb[x],1,n);
            qprint(last);
            putchar('\n');
        }
    }
}

[BZOJ 4771]七彩树(可持久化线段树+树上差分)

原文：https://www.cnblogs.com/birchtree/p/11185814.html