两角和与差的三角函数

1. 概述
   1. 此章节主要是背公式，内容不多，但公式的应用很重要，需要熟记
   2. 本章虽然有许多公式，但核心是两角的和差公式，其他的所有公式都是由和差公式变形产生的
2. 和差公式
   1. $sin(\alpha \pm \beta)=sin \alpha cos \beta \pm cos \alpha sin \beta$
   2. $cos(\alpha \pm \beta)=cos \alpha cos \beta \mp sin \alpha sin \beta$
      1. 已知：如图，$\angle MOQ=\alpha , \angle POQ = \beta$
         求证：$OM=cos(\alpha - \beta)$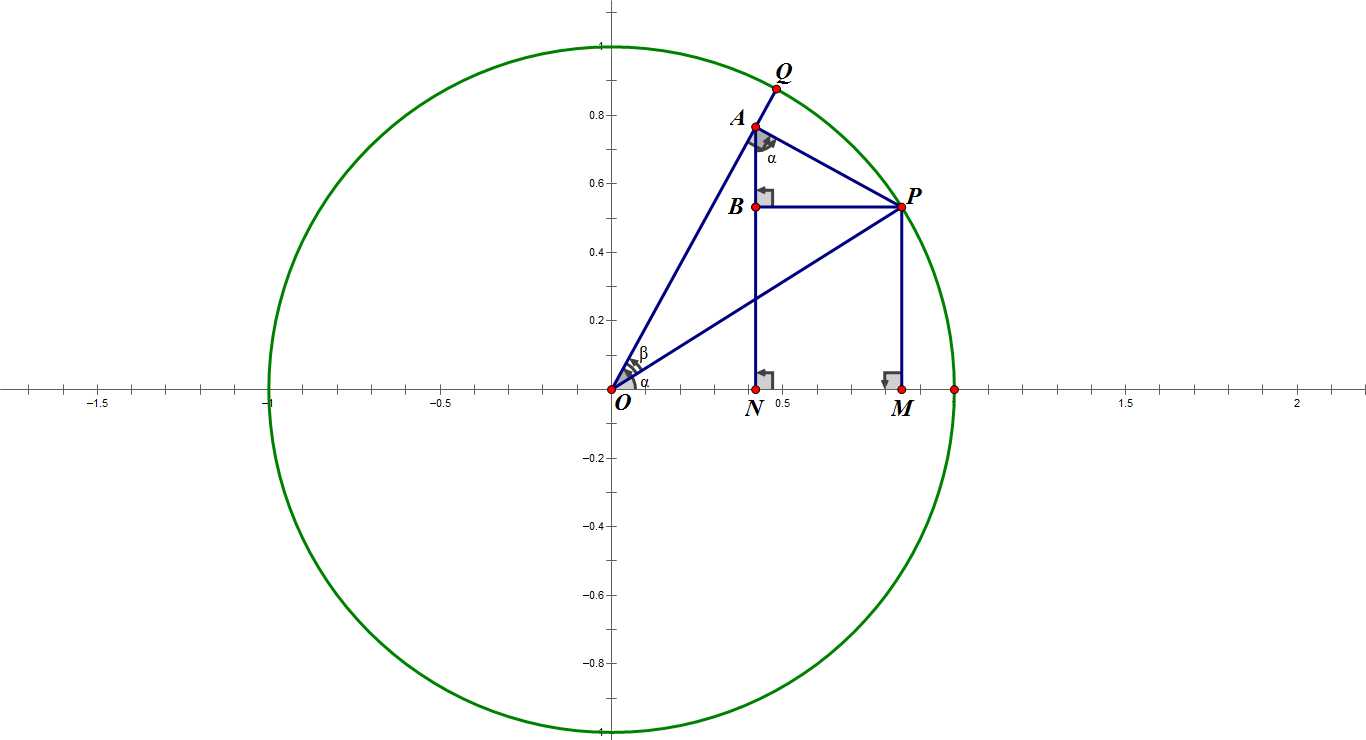

         1. 先将OM拆解成在带有$\alpha$的三角形的边
            $OM=ON+MN$

         2. 将$ON , MN$用$\alpha$表示
            $ON=OA \ast cos \alpha$
            $MN=AP \ast sin \alpha$

         3. 将$OA , AP$用$\beta$表示
            $OA=OP\ast cos \beta$
            $AP=OP\ast sin \beta$

         4. 归并得
            $OM=ON+MN=OP cos \alpha cos \beta + OP sin \alpha sin \beta$
   3. $tan(\alpha \pm \beta)=\frac{tan \alpha \pm tan \beta}{1 \mp tan \alpha tan \beta}$

3. 衍生的公式

   1. 二倍角公式
      将相等的值代入和差公式即可

      1. $sin 2\alpha= 2sin \alpha cos \alpha$

      2. $cos 2\alpha= cos^2 \alpha-sin^2 \alpha=2cos^2 \alpha-1=1-2sin^2\alpha$

      3. $tan 2\alpha=\frac{2 tan \alpha}{1-tan^2\alpha}$

   2. 有关公式的逆用和变形等

      1. $tan \alpha \pm tan \beta= tan(\alpha \pm \beta)(1 \mp tan \alpha tan \beta)$

      2. $cos^2\alpha=\frac{cos 2\alpha+1}{2}　　sin^2 \alpha=\frac{1-cos 2\alpha}{2}$

      3. $1+sin 2a=(sin a+ cos a) 1-2sin 2a=(sin a-cos a)

   3. 辅助角公式

      1. 函数$f(\alpha)= a sin \alpha+ b cos \alpha(a、b为常数)$,可以化为

         1. $f(\alpha)=sqrt{a^2+b^2}sin(\alpha+\phi)(其中tan \phi=\frac{b}{a}$

            1. $\frac{a}{\sqrt{a^2+b^2}}=cos \phi \Rightarrow \frac{b}{\sqrt{a^2+b^2}}=sin \phi$（$\sqrt{a^2+b^2}$是单位一）
            2. $f(\alpha)=a sin \alpha+b sin\alpha$
               $=\sqrt{a^2+b^2}(sin\alpha\ast\frac{a}{sqrt{a^2+b^2}}+cos\alpha\frac{b}{\sqrt{a^2+b^2}})$
               $=\sqrt{a^2}$

         2. $f(\alpha)=sqrt{a^2+b^2}cos(\alpha-\phi)(其中tan \phi=\frac{a}{b}$

两角和与差的三角函数

原文：https://www.cnblogs.com/guoshaoyang/p/11159336.html