题解【UVA12003】Array Transformer

题目描述

输入输出格式

输入格式

输出格式

输入输出样例

输入样例#1

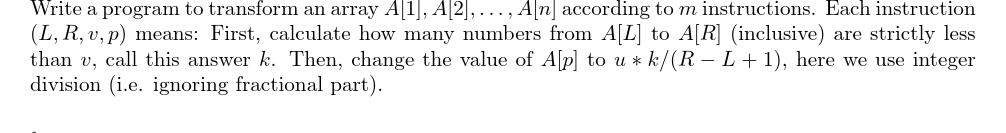
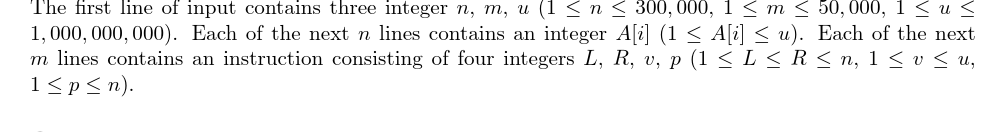
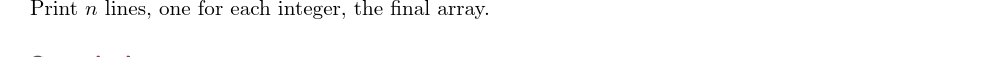
10 1 11
1
2
3
4
5
6
7
8
9
10
2 8 6 10

输出样例#1

1
2
3
4
5
6
7
8
9
6

题意简述

输入一个数组\(a[1,...,n]\)和\(m\)条指令，你的任务是对数组进行变换，输出最终结果。

每条指令形如\((L,R,v,p)\)，表示先统计出\(a[L],a[L+1],...,a[R]\)中严格小于\(v\)的元素个数\(k\)，然后把\(a[p]\)修改成\(u \times k / (R-L+1)\)。这里的除法为整数除法（即忽略小数部分）。

【输入格式】

输入的第一行为\(3\)个整数\(n,m,u(1 \leq n \leq 300 000,1 \leq m \leq 50000 1 \leq u \leq 10^9)\)。

以下\(n\)行为数组\(a[i](1 \leq a[i] \leq u)\)。

再以下\(m\)行每行为\(4\)个整数\(L,R,v,p(1 \leq L \leq R \leq n,1 \leq v \leq u,1 \leq p \leq n)\)。

【输出格式】

输出\(n\)行，每行为一个整数，即变换后的最终数组。

题解

我们可以使用分块法来解决此题。

预设一个整数值\(SIZE\)，然后每\(SIZE\)个元素分成一块，分别排好序，则查询\((L,R,v,p)\)的执行可以分成两步。

第一步，先找出\(L\)和\(R\)所在的块，逐一比较出有多少个元素比\(v\)小，然后对于中间的块直接用二分查找，相加后得到\(k\)。

第二步，在\(p\)所在块中找到修改前的\(a[p]\)，改成\(u \times k/(R-L+1)\)，然后不断交换相邻元素，直到这个块排好序。

根据常识，我们知道，\(SIZE\)的大小在\(\sqrt{n}\)左右比较快，也可以实验得出比较好的\(SIZE\)值。

代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cctype>

using namespace std;

inline int gi()
{
    int f = 1, x = 0;
    char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-') f = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9')
    {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return f * x;
}

const int MAXN = 300000 + 5, SIZE = 4096;//SIZE为块的大小
int a[MAXN], r, block[MAXN / SIZE + 1][SIZE], n, m, u, v;

inline void init()//输入+预处理
{
    n = gi(), m = gi(), u = gi();
    int b = 0, w = 0;
    for (int i = 0; i < n; i++)
    {
        a[i] = gi();//输入每个数
        block[b][w] = a[i];//a[i]为第b个块的第w个元素
        if (++w == SIZE)//这个块是完整的
        {
            ++b;//进入下一个块
            w = 0;
        }
    }
    for (int i = 0; i < b; i++)
    {
        sort(block[i], block[i] + SIZE);//将完整的块排好序
    }
    if (w)
    {
        sort(block[b], block[b] + w);//将边缘块排好序
    }
}

inline int getans(int l, int r, int p)//求出区间内小于v的数的个数
{
    int lft = l / SIZE, rht = r / SIZE, f = 0;
    if (lft == rht)//如果l和r在同一块内
    {
        for (int i = l; i <= r; i++)//直接暴力判断即可
        {
            if (a[i] < v)
            {
                ++f;
            }
        }
        return f;//返回个数
    }
    for (int i = l; i < (lft + 1) * SIZE; i++)//第一块
    {
        if (a[i] < v)
        {
            ++f;
        }
    }
    for (int i = rht * SIZE; i <= r; i++)//最后一块
    {
        if (a[i] < v)
        {
            ++f;
        }
    }
    for (int i = lft + 1; i < rht; i++)//中间块
    {
        f = f + lower_bound(block[i], block[i] + SIZE, v) - block[i];//二分查找
    }
    return f;//返回个数
}

inline void modify(int x, int y)//进行修改
{
    if (a[x] == y)//如果要修改的值就是当前值
    {
        return;//就不用修改,直接返回
    }
    int o = a[x], q = 0, *g = &block[x / SIZE][0];//g就是x所在的块
    a[x] = y;//修改值
    while (g[q] < o)
    {
        ++q;//找到y在块中的位置
    }
    g[q] = y;//进行修改
    if (y > o)//y太大,往后交换
    {
        while (q < SIZE - 1 && g[q] > g[q + 1])
        {
            swap(g[q], g[q + 1]);
            ++q;
        }
    }
    else//x太小,往前交换
    {
        while (q > 0 && g[q] < g[q - 1])
        {
            swap(g[q], g[q - 1]);
            --q;
        }
    }
}

int main()
{
    init();
    while (m--)
    {
        int L, R, p;
        L = gi(), R = gi(), v = gi(), p = gi();
        --L, --R, --p;
        int z = getans(L, R, v);//求出区间内比v小的数
        modify(p, (long long)u * z / (R - L + 1));//进行修改
    }
    for (int i = 0; i < n; i++)
    {
        printf("%d\n", a[i]);//输出每个数
    }
    return 0;//结束
}

题解【UVA12003】Array Transformer

原文：https://www.cnblogs.com/xsl19/p/11149989.html