
>> A=[2 1 3;1 3 2];B=[5;10]
B =
5
10
>> X=lsqnonneg(A,B)
X =
0
2.8571
0.7143
>> A\B
ans =
0
2.8571
0.7143

>> p=[1 -7 10] %表示x^2-7x+10
p =
1 -7 10
>> r=roots(p)
r =
5
2
>> p=poly(r)%由根创建多项式
p =
1 -7 10
>> A=ones(3),poly(A)
A =
1 1 1
1 1 1
1 1 1
ans =
1.0000 -3.0000 -0.0000 -0.0000
>> d=eig(A),[v,d]=eig(A) %求方阵A的特征值d与特征向量
d =
-0.0000
-0.0000
3.0000
v =
0.4082 0.7071 0.5774
0.4082 -0.7071 0.5774
-0.8165 0 0.5774
d =
-0.0000 0 0
0 -0.0000 0
0 0 3.0000
>> a=[1 -2],b=[1 -5],c=polyder(a,b) %多项式a和b乘积的导数
a =
1 -2
b =
1 -5
c =
2 -7
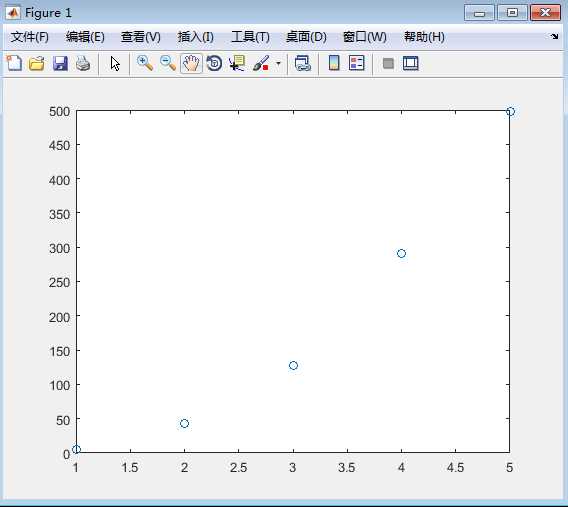
>> x=[1 2 3 4 5],y=[5.5 43.1 128 290.7 498.4]
x =
1 2 3 4 5
y =
5.5000 43.1000 128.0000 290.7000 498.4000
>> plot(x,y,‘o‘)
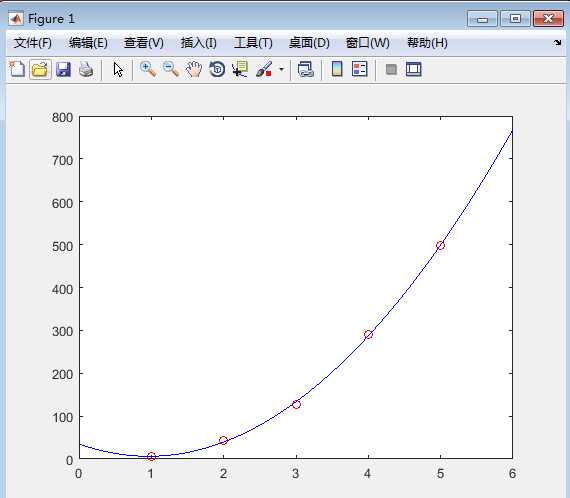
>> p = polyfit(x,y,3)
p =
-0.1917 31.5821 -60.3262 35.3400
>> xi=0:0.02:6;
>> yi=polyval(p,xi);
>> plot(x,y,‘ro‘,xi,yi,‘b-‘)
>>

>> fun=@(x) 2*sin(x)-1
fun =
@(x)2*sin(x)-1
>> [x,f]=fminbnd(fun,3,6) %y=f(x)在指定区间[a,b]上的局部极小值指令为: [x,f]=fminbnd(fun,a,b);返回取极小值时自变量值x与函数值f_
x =
4.7124
f =
-3.0000
>> funf=@(x) x(1)^2+2.5*sin(x(2))-x(1)*x(2)^2*x(3)^2
funf =
@(x)x(1)^2+2.5*sin(x(2))-x(1)*x(2)^2*x(3)^2
>> [x,f]=fminsearch(funf,[1,-1,0]) %猜一个初始值,从这个点开始找局部最小值
x =
-0.0000 -1.5708 0.0008
f =
-2.5000
>> z=@(x,a,b) a*sin(x(1))+b*cos(x(2))
z =
@(x,a,b)a*sin(x(1))+b*cos(x(2))
>> [x,f]=fminsearch(@(x) z(x,2,1),[0,0]) %将一个新匿名函数做参数传入
x =
-1.5708 3.1416
f =
-3.0000
>>

MATLAB学习(四)线性方程求解,多项式运算,函数局部最优解
原文:https://www.cnblogs.com/caiyishuai/p/11150094.html