故事的开始是leetcode的一道Mid难度题1109. Corporate Flight Bookings
一开始做这道题我就直接暴力遍历和加法,结果当然直接超时(qwq蒟蒻的哭泣)。
于是看了一下午线段树,结果这道题也不用自己构建树,因为不涉及区间查询,直接从头到位输出就可以了。
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
const int N = 20000 + 5;
vector<int>t;
int arr[N];//存储首位订票信息
memset(arr, 0, sizeof(arr));
for (int i = 0; i < bookings.size(); i++)//更新首位信息
{
arr[bookings[i][0]] += bookings[i][2];
arr[bookings[i][1]+1] -= bookings[i][2];
}
int ans = 0;
for (int i = 1; i <= n; i++)//取出更新
{
ans += arr[i];
t.push_back(ans);
}
return t;
}
};那么问题来了,如果要区间查找该怎么办?如果按照上面的算法,先将ans存储下来,再按照题意去查询,相加的话应该是相当耗时的,所以这个时候就不得不去搭建一棵\(线段树\color{red}{线段树}\)。
\(线段树\color{red}{线段树}\)的核心是二分。
它有以下两点重要的性质:
这是线段树的结构:
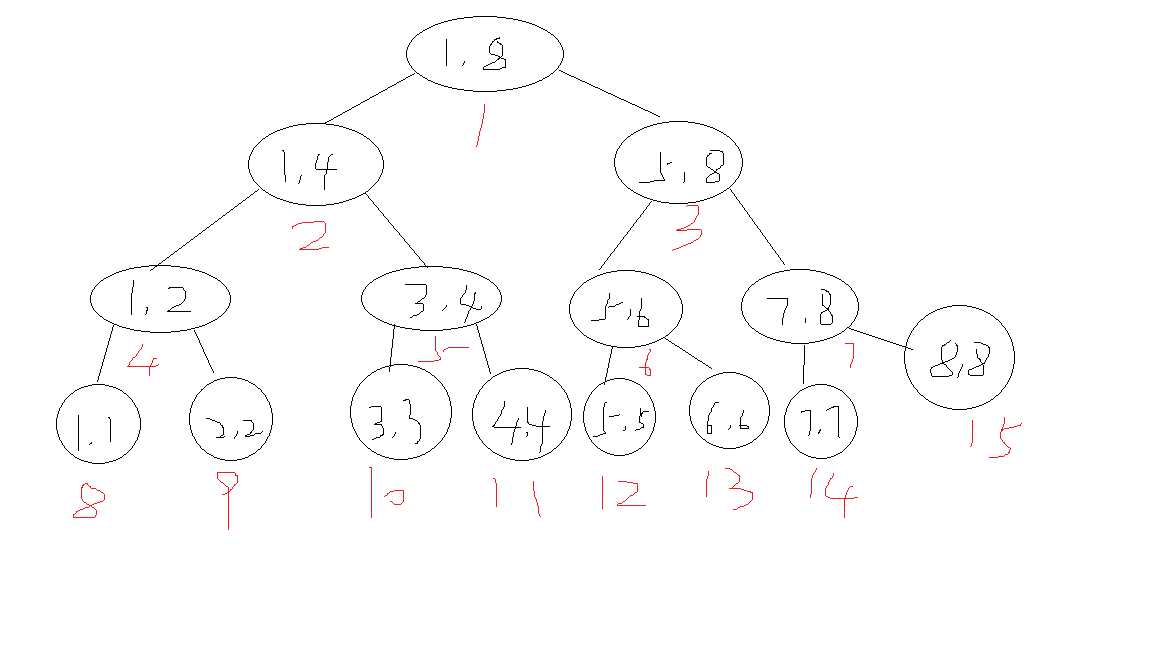
然后是线段树节点的结构体定义:
struct node
{
int l, r, v, f;//左,右区间,存储的值,懒标记(区间查询的时候有用)
}tree[4*n];//要构造至少4*n的空间,为什么?待考虑。。。那首先来构建一棵线段树:
void build(int l,int r,int k)
{
tree[k].l = l;//左区间赋值
tree[k].r = r;//右区间赋值
if (l == r)//当到达叶子节点的时候给叶子赋值,即给每一个具体的点赋值如(1,1)
{
scanf("%d", &tree[k].v);
return;
}
int mid = (l + r) / 2;//找中点
build(l, mid, k * 2);//构造左孩子
build(mid + 1, r, k * 2 + 1);//构造右孩子
tree[k].v = tree[k * 2].v + tree[k * 2 + 1].v;//值的合并
}单点查询:
void ask(int k,int x)//k为根节点,x是要查询的点
{
if(tree[k].l==tree[k].r) //是叶子节点就是最后的答案
{
ans=tree[k].v;
return;
}
int mid=(tree[k].l+tree[k].r)/2;
if(x<=mid)
ask(k*2);//目标位置比中点靠左,就递归左孩子
else
ask(k*2+1);//反之,递归右孩子
}单点修改:
void one_add(int k,int x,int v)//k为根节点,x为要查询的点,v为要增加的值
{
if (tree[k].l == tree[k].r)//是叶子节点就是要修改的节点
{
tree[k].v += v;
return;
}
int mid = (tree[k].l + tree[k].r) / 2;//中点值
if (x <= mid)
one_add(k * 2, x, v);
else
one_add(k * 2 + 1, x, v);
tree[k].v = tree[k * 2].v + tree[k * 2 + 1].v;
}区间查询(求和):
void sum(int k, int a, int b)
{
if (tree[k].l >= a && tree[k].r <= b)//如果要查询的区间被包含,那么就加上区间值,然后返回
{
ans += tree[k].v;
return;
}
int mid = (tree[k].l + tree[k].r) / 2;
if(a<=mid)//可以理解一下,因为这个比较是在一直再细分区间,所以才会两个if来划分判断
sum(k * 2, a, b);
if(b>mid)
sum(k * 2 + 1, a, b);
}区间修改:
所以这时候就要引入一个新的概念 ,懒标记,用来存储修改的累计,等到下一次修改或者查询的时候再将懒标记用在下面。
void down(int k)
{
tree[k*2].f+=tree[k].f;
tree[k*2+1].f+=tree[k].f;
tree[k*2].w+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);//区间长度*懒节点的值
tree[k*2+1].w+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);
tree[k].f=0;//父亲节点懒节点清零
}void add(int k)
{
if(tree[k].l>=a&&tree[k].r<=b)//当前区间在要修改的区间内
{
tree[k].w+=(tree[k].r-tree[k].l+1)*x;//(r-1)+1区间点的总数
tree[k].f+=x;//给当前懒标记赋值,不接着向下修改了
return;
}
if(tree[k].f)
down(k);//懒标记下传。
int mid=(tree[k].l+tree[k].r)/2;
if(a<=mid)
add(k*2);
if(b>mid)
add(k*2+1);
tree[k].w=tree[k*2].w+tree[k*2+1].w;//更改区间状态
}如果引入懒节点,那么单点修改,单点查询,区间查询代码都要作相应改动:
void sum(int k, int a, int b)
{
if (tree[k].l >= a && tree[k].r <= b)//如果要查询的区间被包含,那么就加上区间值,然后返回
{
ans += tree[k].v;
return;
}
if(tree[k].f)
down(k);//增加懒标记下传
int mid = (tree[k].l + tree[k].r) / 2;
if(a<=mid)//可以理解一下,因为这个比较是在一直再细分区间,所以才会两个if来划分判断
sum(k * 2, a, b);
if(b>mid)
sum(k * 2 + 1, a, b);
}void ask(int k,int x)//k为根节点,x是要查询的点
{
if(tree[k].l==tree[k].r) //是叶子节点就是最后的答案
{
ans=tree[k].v;
return;
}
if(tree[k].f)
down(k);//增加懒标记下传
int mid=(tree[k].l+tree[k].r)/2;
if(x<=mid)
ask(k*2);//目标位置比中点靠左,就递归左孩子
else
ask(k*2+1);//反之,递归右孩子
}void sum(int k, int a, int b)
{
if (tree[k].l >= a && tree[k].r <= b)//如果要查询的区间被包含,那么就加上区间值,然后返回
{
ans += tree[k].v;
return;
}
if(tree[k].f)
down(k);//增加懒标记下传
int mid = (tree[k].l + tree[k].r) / 2;
if(a<=mid)//可以理解一下,因为这个比较是在一直再细分区间,所以才会两个if来划分判断
sum(k * 2, a, b);
if(b>mid)
sum(k * 2 + 1, a, b);
}原文:https://www.cnblogs.com/JMWan233/p/11147270.html