最基础的:
\(C^{m}_{n}=\frac{n!}{m!(n-m)!}\)
他的逆元算法是:
因为阶乘是\(fac[i]=fac[i-1]*i\)
所以阶乘逆元是\(invfac[n]=fac[n]^{p-2}\)
=>\(invfac[i-1]=invfac[i]*i\)
于是\(\color{#00CCFF}{C^{m}_{n}=fac[n]*invfac[n-m]%p*invfac[m]%p}\)
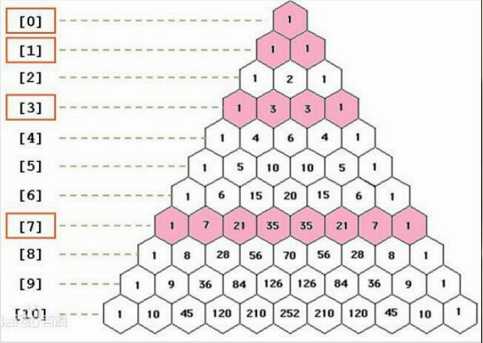
若将\(C^{m}_{n}\)分行我们就得到了伟大的杨辉Triangle!
原文:https://www.cnblogs.com/ComputerEngine/p/11146306.html