线段树(SegmentTree)是一种基于分治思想的二叉树结构,用于区间上进行信息统计。与按照二进制位进行划分的树状数组相比,线段树是一种更加通用的结构。
性质
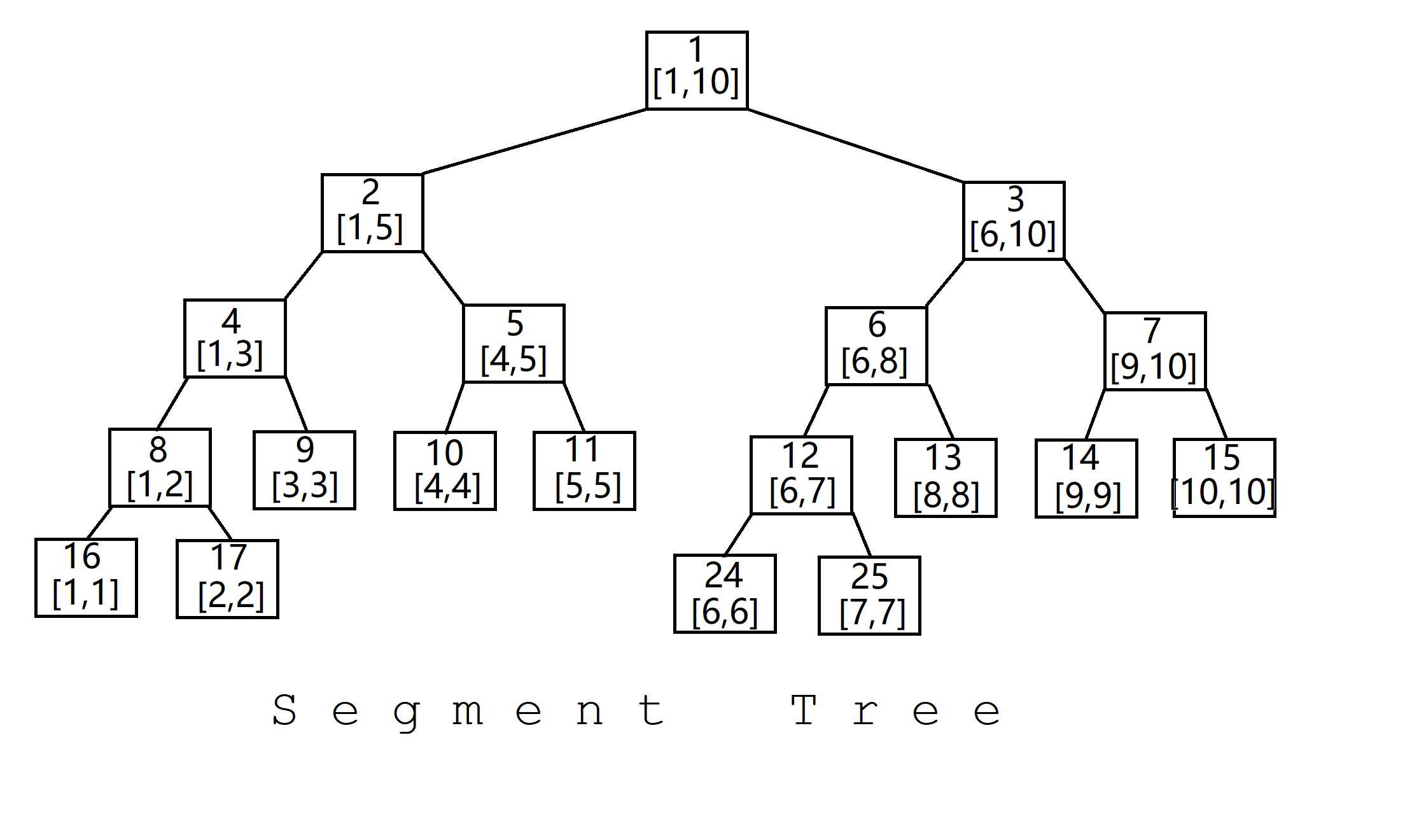
建树
每个叶节点t[i, i]维护a[i]的值,从而使信息从下向上传递信息。
单点更改
从根节点出发,找到区间[x, x]的叶节点,然后从下向上更新。
区间查询
延迟标记
区间修改的指令中,某个区间的结点改变,整棵子树中的所有节点存储的信息都会发生变化,修改的时间复杂度将会增加到O(N)。
我们发现,若我们将区间的整棵子树进行更新,却始终没有进行查询,那么整棵子树的更新都是徒劳的。所以,我们可以在修改指令时找到完全覆盖的区间后立即返回,只是在其中增加一个标记,表示此节点已经更改,但子树都未更新。
此后的更改和查询命令中,在向下访问之前,我们先将未更新的结点向下传递,然后清除当前结点的标记。这样一来,时间复杂度仍可维持在O(logN)。
模板:
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.求出某区间每一个数的和
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
1 #include<iostream> 2 using namespace std; 3 const int SIZE = 100005; 4 struct SegmentTree{ 5 int l, r; 6 long long add, sum; 7 }t[SIZE*4]; 8 int a[SIZE], n, m; 9 10 void build(int p, int l, int r){ 11 t[p].l = l, t[p].r = r; 12 if(l == r){ 13 t[p].sum = a[l]; 14 return; 15 } 16 int mid = (l + r) >> 1; 17 build(p*2, l, mid); 18 build(p*2+1, mid+1, r); 19 t[p].sum = t[p*2].sum + t[p*2+1].sum; 20 } 21 22 void spread(int p){ 23 if(t[p].add){ //结点p有标记 24 t[p*2].sum += t[p].add * (t[p*2].r-t[p*2].l+1); 25 t[p*2+1].sum += t[p].add * (t[p*2+1].r-t[p*2+1].l+1); 26 t[p*2].add += t[p].add; //延迟标记 27 t[p*2+1].add += t[p].add; 28 t[p].add = 0; 29 } 30 } 31 32 void change(int p, int l, int r, int d){ 33 if(l <= t[p].l && r >= t[p].r){ 34 t[p].sum += (long long)d * (t[p].r - t[p].l + 1); 35 t[p].add += d; 36 return; 37 } 38 spread(p); 39 40 int mid = (t[p].l + t[p].r) >> 1; 41 if(l <= mid) change(p*2, l, r, d); 42 if(r > mid) change(p*2+1, l, r, d); 43 t[p].sum = t[p*2].sum + t[p*2+1].sum; 44 } 45 46 long long ask(int p, int l, int r){ 47 if(l <= t[p].l && r >= t[p].r) return t[p].sum; 48 spread(p); 49 int mid = (t[p].l + t[p].r) >> 1; 50 long long val = 0; 51 if(l <= mid) val += ask(p*2, l, r); 52 if(r > mid) val += ask(p*2+1, l, r); 53 return val; 54 } 55 56 int main(){ 57 cin >> n >> m; 58 for(int i=1; i<=n; i++) cin >> a[i]; 59 build(1, 1, n); 60 while(m--){ 61 int k, l, r, h; 62 cin >> k >> l >> r; 63 switch(k){ 64 case 1: 65 cin >> h; 66 change(1, l, r, h); 67 break; 68 case 2: 69 cout << ask(1, l, r) <<"\n"; 70 break; 71 } 72 } 73 return 0; 74 }
原文:https://www.cnblogs.com/hnoi/p/11144490.html