题目说明在这里就不贴出来了,相信打开这篇文章的小伙伴们肯定都是在刷LeetCode的。
一开始我的想法是dfs+回溯,结果运行超时,一开始我就觉得可能会超时,结果不出所料【手动笑哭】。
后来我想了下dfs在每一次都需要遍历,这样时间复杂度当然高啊。
后来经过了不知道多久的好久,我就学会了使用动态规划的方法,哎,动态规划一直是我的弱点所在,逻辑思维能力跟不上!
动态规划的重点在于找到状态转换方程,说是这样说的,但是我每次都找不到转换方程啊。。。。哈哈哈哈,无奈大笑!
废话不多,直接上图,一图胜千言!
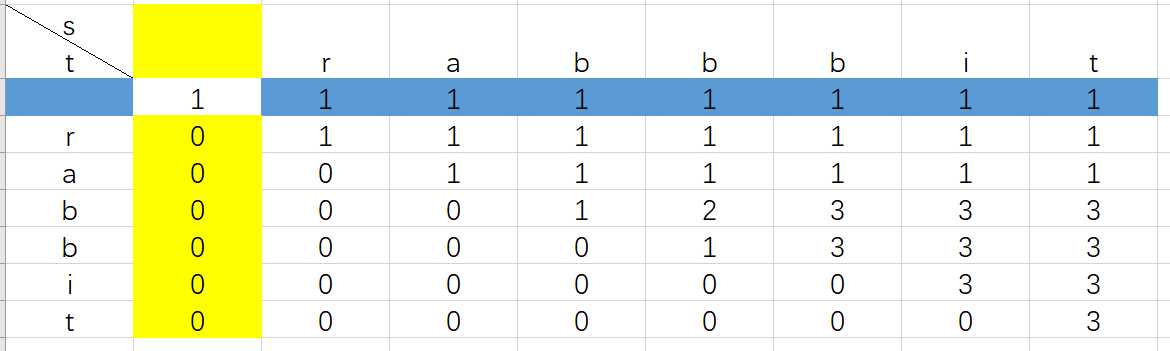
解释上图:各位小伙伴可以发现蓝色一行全为1,啥意思尼?因为我们设置dp[t.length+1][s.length+1],多一行
和多一列的目的是我们需要dp【0】【0】的那个初始值1,因为当 s 为空 t 为空时匹配情况为1,然后当 t 为空随
着 s 不断变长其匹配数仍为1。黄色一列同理可得当 s 为空 t 不空时没有可以匹配的。
然后我们通过观察可以猜出
if(t【i-1】== s【j-1】)dp【i】【j】 = dp【i-1】【j-1】+ dp【i】【j-1】
else dp【i】【j】 = dp【i】【j-1】
else后面的很好理解,例如当 t 取前面一个字符 “r” 然后依次从前往后去s中找匹配,当 s = “r”时匹配为1, 当 s = “ra”
时匹配仍为1,依次类推。
然而,if后面的那个表达式又是什么意思呢?

如图,这个例子可以很好的解释,现在要求最后一个方框中的值,dp【i】【j】 = dp【i-1】【j-1】+ dp【i】【j-1】
在这里的解释就是:在a之前b的个数,有多少个b就可以与a组成多少对匹配,
然后加上当s = “ba” s = “babagc” 时,能够匹配的ba的数量
原文:https://www.cnblogs.com/jiguang321/p/11129304.html