【输入输出样例 1】
|
ilove.in |
ilove.out |
|
1 3 2 19260718 |
2 |
见选手文件夹下的 Samples/ilove/ilove1.in 和Samples/ilove/ilove1.ans。
【输入输出样例1解释】
一共有两朵花,3 个位置。如果给花朵编号为 1,2,位置编号为 1,2,3,那么两种方案分别如下:
|
位置 |
1 |
2 |
3 |
|
方案1 |
花朵1 |
N/A |
花朵2 |
|
方案2 |
花朵2 |
N/A |
花朵1 |
【输入输出样例 2】
见选手文件夹下的 Samples/ilove/ilove2.in 和Samples/ilove/ilove2.ans。
【数据规模与约定】
|
子任务编号 |
n≤ |
m≤ |
type= |
特殊性质 |
子任务分值 |
|
1 |
1 |
1 |
0 |
特殊性质1 |
5 |
|
2 |
20 |
20 |
1 |
15 |
|
|
3 |
400 |
200 |
2 |
无 |
20 |
|
4 |
2000 |
1000 |
3 |
||
|
5 |
2000000 |
1000000 |
4 |
特殊性质2 |
|
|
6 |
5 |
无 |
特殊性质1:保证对应测试点的实际方案数(在取模之前)不超过106
特殊性质2:保证对应测试点的模数 p 是一个质数。定义整数 x 为一个质数当且仅当 x 有且仅有 1 和 x 两个因数。
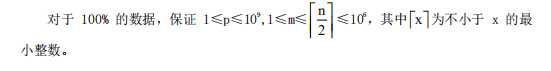
题解:
我们现在有n个位置,放m个物品,考虑把放了物品的位置拿出来,还剩下n-m个空着的位置(这些位置是不能放东西的),然后把这m个物品插入到这n-m个位置所夹的空位里面(插空法),加上两边一共n-m+1个位置,所以所有放的位置的情况就是Cn-m+1m然后在乘上他自己的全排列Amm,化简之后就是!(n-m+1)/!(n-2m+1)=∏n-2m+2n-m+1
代码。。。
都化简成这样了,还不会吗QωQ
原文:https://www.cnblogs.com/lcezych/p/11093143.html