Description
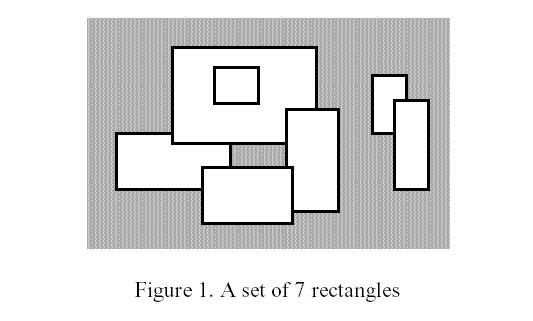
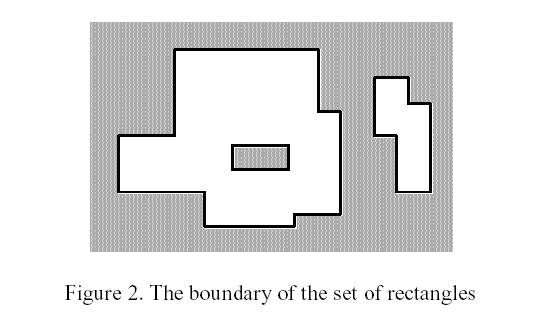
Input
Output
Sample Input
7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
Sample Output
228
第一种,对横向纵向分别遍历,用两次扫描线,第一次从左到右,离散化y坐标,增加一条边后,引起总和改变,改变量就是边的长度,没改变的就是隐藏在了原来图形的里面,没有形成新的边,先把所有纵向的边总计,在统计横向的边,最后的结果就是总的边长。也可以避免求图形内部的边。
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
#define maxn 11000
struct node{
int l , r ;
int sum ;
}cl[maxn<<2];
struct node1{
int k , l , r ;
int flag ;
}p[maxn] , q[maxn];
int lazy[maxn<<2] , x[maxn] , y[maxn] ;
bool cmp(node1 a,node1 b)
{
return a.k < b.k ;
}
void push_up(int rt)
{
if( lazy[rt] )
cl[rt].sum = cl[rt].r - cl[rt].l ;
else
cl[rt].sum = cl[rt<<1].sum + cl[rt<<1|1].sum ;
}
void creat(int rt,int l,int r,int *a)
{
cl[rt].l = a[l] ;
cl[rt].r = a[r] ;
if( r - l > 1 )
{
creat(rt<<1,l,(l+r)>>1,a);
creat(rt<<1|1,(l+r)>>1,r,a);
push_up(rt);
}
else
cl[rt].sum = 0 ;
return ;
}
void update(int rt,int l,int r,int flag)
{
if( cl[rt].l == l && cl[rt].r == r )
{
lazy[rt] += flag ;
push_up(rt);
}
else
{
if( cl[rt<<1].r > l ){
int x = min(cl[rt<<1].r,r) ;
update(rt<<1,l,x,flag);}
if( cl[rt<<1|1].l < r ){
int x = max(cl[rt<<1|1].l,l) ;
update(rt<<1|1,x,r,flag);}
push_up(rt);
}
}
int main()
{
int i , j , n , m , x1 , y1 , x2 , y2 , low , ans ;
while(scanf("%d", &n)!=EOF)
{
for(i = 0 ; i < n ; i++)
{
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
p[i].k = x1 ;p[i].l = y1 ;p[i].r = y2 ;p[i].flag = 1 ;
p[i+n].k = x2 ;p[i+n].l = y1 ;p[i+n].r = y2 ;p[i+n].flag = -1 ;
y[i+1] = y1 ;
y[i+n+1] = y2 ;
q[i].k = y1 ;q[i].l = x1 ;q[i].r = x2 ;q[i].flag = 1 ;
q[i+n].k = y2 ;q[i+n].l = x1 ;q[i+n].r = x2 ;q[i+n].flag = -1 ;
x[i+1] = x1 ;
x[i+n+1] = x2 ;
}
ans = 0 ;
memset(lazy,0,sizeof(lazy));
sort(y+1,y+(2*n+1));
sort(p,p+2*n,cmp);
m = unique(y+1,y+(2*n+1))- (y+1);
creat(1,1,m,y);
ans = low = 0 ;
update(1,p[0].l,p[0].r,p[0].flag);
ans += fabs(low-cl[1].sum);
low = cl[1].sum ;
for(i = 1 ; i < 2*n ; i++)
{
update(1,p[i].l,p[i].r,p[i].flag);
ans += fabs(low - cl[1].sum);
low = cl[1].sum ;
}
sort(q,q+2*n,cmp);
sort(x+1,x+(2*n+1));
m = unique(x+1,x+(2*n+1))-(x+1);
memset(lazy,0,sizeof(lazy));
memset(cl,0,sizeof(cl));
creat(1,1,m,x);
low = 0 ;
update(1,q[0].l,q[0].r,q[0].flag);
ans += fabs(low-cl[1].sum);
low= cl[1].sum ;
for(i = 1 ; i < 2*n ; i++)
{
update(1,q[i].l,q[i].r,q[i].flag);
ans += fabs( low - cl[1].sum );
low = cl[1].sum ;
}
printf("%d\n", ans);
}
return 0;
}第二种。第一种用了两次扫描线比较麻烦,也可以只用一次扫描线,离散y坐标,按x从左到右扫描,统计每次总和的更改值,这样可以得到所有纵向边的和,对于横向边,可以用(p[i].k - p[i-1].k)*cl[1].num*2.前面的(p[i].k - p[i-1].k)相邻的两条线段的x坐标的差,cl[1].num代表此时在线段树中一共有几条线段,每一条线段,就会增加这条线段的两个端点带来的横边。所以只要统计到当时有多少段覆盖的边,就可以得到那一段的横向的增加值
统计某一时刻有多少线段覆盖,可以用lp , rp记录这一个节点的两个端点是不是已经覆盖,如果覆盖值为1,那么这一段的num就是1,合并两个节点的时候,父节点的num等于左右子节点的num和,如果左节点的rp与右节点的lp都是1,那么父节点的num值减去1。最后得到统计整个线段是由几个线段组成。
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
#define maxn 11000
struct node{
int k , l , r , flag ;
} p[maxn];
struct node1{
int l , r , lp , rp ;
int sum , num ;
} cl[maxn<<2];
int lazy[maxn<<2] , s[maxn] ;
bool cmp(node a,node b)
{
return a.k < b.k ;
}
void push_up(int rt)
{
if( lazy[rt] )
{
cl[rt].lp = cl[rt].rp = 1 ;
cl[rt].num = 1 ;
cl[rt].sum = cl[rt].r - cl[rt].l ;
}
else
{
cl[rt].sum = cl[rt<<1].sum + cl[rt<<1|1].sum ;
cl[rt].num = cl[rt<<1].num + cl[rt<<1|1].num ;
cl[rt].lp = cl[rt<<1].lp ; cl[rt].rp = cl[rt<<1|1].rp ;
if( cl[rt<<1].rp && cl[rt<<1|1].lp )
cl[rt].num-- ;
}
}
void creat(int rt,int l,int r)
{
cl[rt].l = s[l] ;
cl[rt].r = s[r] ;
cl[rt].lp = cl[rt].rp = 0 ;
if( r - l > 1 )
{
creat(rt<<1,l,(l+r)/2);
creat(rt<<1|1,(l+r)/2,r);
push_up(rt);
}
else
cl[rt].num = cl[rt].sum = 0 ;
}
void update(int rt,int l,int r,int flag)
{
if( cl[rt].l == l && cl[rt].r == r )
{
lazy[rt] += flag ;
push_up(rt);
}
else
{
if( cl[rt<<1].r > l ){
int x = min(r,cl[rt<<1].r) ;
update(rt<<1,l,x,flag);}
if( cl[rt<<1|1].l < r ){
int x = max(l,cl[rt<<1|1].l) ;
update(rt<<1|1,x,r,flag);}
push_up(rt);
}
return ;
}
int main()
{
int n , m , i , j , x1 , y1 , x2 , y2 , ans , low ;
while(scanf("%d", &n)!=EOF)
{
for(i = 0 ; i < n ; i++)
{
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
p[i].k = x1 ; p[i].l = y1 ; p[i].r = y2 ;p[i].flag = 1 ;
p[i+n].k = x2 ;p[i+n].l = y1 ; p[i+n].r = y2 ; p[i+n].flag = -1 ;
s[i+1] = y1 ;
s[i+n+1] = y2 ;
}
sort(s+1,s+(2*n+1));
sort(p,p+2*n,cmp);
m = unique(s+1,s+(2*n+1))-(s+1) ;
memset(lazy,0,sizeof(lazy));
creat(1,1,m);
ans = 0 ;
low = 0 ;
update(1,p[0].l,p[0].r,p[0].flag);
ans += fabs( low - cl[1].sum );
low = cl[1].sum ;
for(i = 1 ; i < 2*n ; i++)
{
ans += ( p[i].k - p[i-1].k )*cl[1].num*2 ;
update(1,p[i].l,p[i].r,p[i].flag);
ans += fabs( low - cl[1].sum );
low = cl[1].sum ;
}
printf("%d\n", ans);
}
return 0;
}
hdu1828 Picture(线段树+离散化+扫描线)两种方法,布布扣,bubuko.com
hdu1828 Picture(线段树+离散化+扫描线)两种方法
原文:http://blog.csdn.net/winddreams/article/details/38520833