说来惭愧,一个月前就写了tire的题,现在才想起来整理博客,中途我会隔一段时间在敲一下原来做过的题,能做到速度和质量后再来写一下我的一些心得吧;
Tire树:一种基本的数据结构;(这里先不写可持久化tire树)
用来实现字符串快速检索的一种多叉树,每个节点拥有多个字符指针,若在插入或检索中扫描到一个字符c,沿着当前指针走向指针所指的下一个节点;
1.初始化:只有一个根节点,字符指针均指向空;
2.插入:插入一个字符串s;
首先建一个指针P指向根节点,扫描每一个字符c,若P的c字符指针指向节点Q,那么令P=Q;
如果P的c字符指针指向空,那么新建一个节点Q,令P=Q
依次扫描,直至在字符串的末尾(当前的P节点)标记一下;
3,查询:查过一个字符串S是否在tire中出现过;
从根节点出发,扫描S的每一个字符c,如果当前指针P的c字符指针指向空,那么结束,S没有出现过;
如果扫描完S的每一个字符后,当前指针P被标记过,那么S出现过,否则没有出现过;
以上是tire的基本操作;
此类问题也常与前缀问题,异或问题结合,下面会接着讲;
1.前缀统计
题目描述:
给定N个字符串S1,S2…SN,接下来进行M次询问,每次询问给定一个字符串T,求S1~SN中有多少个字符串是T的前缀。
第一行输入两个整数N,M。
接下来N行每行输入一个字符串SiSi。
接下来M行每行一个字符串T用以询问。
对于每个询问,输出一个整数表示答案。
每个答案占一行。
思路:
我们将N个字符串插入tire树中,但是我们为了处理重复现象,我们将每个节点记录为有多少个字符串的在这里结尾,记录个数cnt,而不能只做结尾标记;
检索字符串T,累加路径上的cnt即可;

#include<bits/stdc++.h> using namespace std; #define N 1000010 int idx,n,m; int tire[N][26],cnt[N]; string s; template<typename T>inline void read(T &x) { x=0;T f=1,ch=getchar(); while(!isdigit(ch)) {if(ch==‘-‘) f=-1; ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48); ch=getchar();} x*=f; } inline void insert(string s) { int p=0; for(int i=0;i<s.size();i++) { int ch=s[i]-‘a‘; if(tire[p][ch]==0) tire[p][ch]=++idx; p=tire[p][ch]; } cnt[p]++; } inline int query(string s) { int p=0,res=0; for(int i=0;i<s.size();i++) { p=tire[p][s[i]-‘a‘]; if(p==0) return res; res+=cnt[p]; } return res; } int main() { read(n);read(m); for(int i=0;i<n;i++) { cin>>s; insert(s); } for(int i=0;i<m;i++) { cin>>s; cout<<query(s)<<endl; } return 0; }
题目描述:
在给定的N个整数A1,A2……ANA1,A2……AN中选出两个进行xor(异或)运算,得到的结果最大是多少?
第一行输入一个整数N。
第二行输入N个整数A1A1~ANAN。
输出一个整数表示答案。
1≤N≤105
0≤Ai<231
思路:
枚举是行不通了;
根据XOR的性质是“相同为0,不同为1”,我们再选两个数异或时尽量选择每位不同的,尽可能的让结果大;
所以我们将每个数看做一个二进制数插入tire树中;
接下来对应每一个Ai,我们进行检索;
怎么检索呢,我们从根节点出发,对于当前Ai的j位,我们每次都尝试沿着与j位上数字的不同的指针向下检索,(这样答案尽可能大),
如果与其不同的指针指向空,那么我么只好沿着相同的走;
这样我们就找到了与当前Ai做XOR最大的值了;

#include<bits/stdc++.h> using namespace std; #define N 1000100 #define M 3000000 int n,a[N],tire[M][2],idx; template<typename T>inline void read(T &x) { x=0;T f=1,ch=getchar(); while(!isdigit(ch)) {if(ch==‘-‘) f=-1; ch=getchar();} while(isdigit(ch)) {x=x*10+ch-‘0‘; ch=getchar();} x*=f; } inline void insert(int x) { int p=0; for(int i=31;~i;i--) { int ch=x>>i&1; if(tire[p][ch]==0) tire[p][ch]=++idx; p=tire[p][ch]; } } inline int query(int x) { int p=0,res=0; for(int i=31;~i;i--) { int ch=x>>i&1; if(tire[p][ch^1]) { p=tire[p][ch^1]; res+=1<<i; } else p=tire[p][ch]; } return res; } int main() { read(n); for(int i=1;i<=n;i++) { read(a[i]); insert(a[i]); } int ans=0; for(int i=1;i<=n;i++) ans=max(ans,query(a[i])); cout<<ans<<endl; }
题目描述:
给定一个树,树上的边都具有权值。
树中一条路径的异或长度被定义为路径上所有边的权值的异或和:
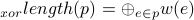
⊕ 为异或符号。
给定上述的具有n个节点的树,你能找到异或长度最大的路径吗?
第一行包含整数n,表示树的节点数目。
接下来n-1行,每行包括三个整数u,v,w,表示节点u和节点v之间有一条边权重为w。
输出一个整数,表示异或长度最大的路径的最大异或和。
1≤n≤100000
0≤u,v<n
0≤w<231
思路:
设D[x]为根节点到x的路径上所有边权的XOR值;
那么有:D[x]=D[father[x]]xorWeight(x,father(x));
根据上式,我们可以先dfs求出当前所有节点的D[x]值,那么x到y的路径就是D[x]xorD[y],(即使没有经过根节点,那么重复的相同路径异或后为0,所以将相当于没有经过);
所以问题转化:
从D[1]~D[N]中选择两个使得XOR值最大,和上题类似;
同样使用tire树快速求解:
但是洛谷和Acwing的根节点不同,以下是Acwing的AC代码;

#include<bits/stdc++.h> using namespace std; #define N 500010 #define M 3000010 template<typename T>inline void read(T &x) { x=0;T f=1,ch=getchar(); while(!isdigit(ch)) {if(ch==‘-‘) f=-1; ch=getchar();} while(isdigit(ch)) {x=x*10+ch-‘0‘; ch=getchar();} x*=f; } int n,x,y,z,tot,idx,lin[N],d[M],tire[M][2]; struct gg{ int y,next,v; }a[N<<1]; inline void add(int x,int y,int v) { a[++tot].y=y; a[tot].next=lin[x]; a[tot].v=v; lin[x]=tot; } inline void dfs(int x,int fa,int sum) { d[x]=sum; for(int i=lin[x];i;i=a[i].next) { int y=a[i].y; if(y!=fa) { dfs(y,x,sum^a[i].v); } } } inline void insert(int x) { int p=0; for(int i=31;~i;i--) { int ch=x>>i&1; if(tire[p][ch]==0) tire[p][ch]=++idx; p=tire[p][ch]; } } inline int query(int x) { int p=0,res=0; for(int i=31;~i;i--) { int ch=x>>i&1; if(tire[p][ch^1]) { p=tire[p][ch^1]; res+=1<<i; } else p=tire[p][ch]; } return res; } int main() { read(n); for(int i=1;i<n;i++) { read(x);read(y);read(z); add(x,y,z); add(y,x,z); } dfs(0,-1,0); for(int i=1;i<=n;i++) { insert(d[i]); } int ans=0; for(int i=1;i<=n;i++) ans=max(ans,query(d[i])); printf("%d\n",ans); return 0; }
ok撒~;
原文:https://www.cnblogs.com/Tyouchie/p/11009008.html