这篇文章主要讲解八叉树算法的原理,并用java进行实现
八叉树最早是在1988年,由 M. Gervautz 和 W. Purgathofer 提出,该算法的最大优点是效率高,占用内存少。在图像量化中的思路是,图像rgb通道的值均为8比特的二进制数,数字所在的比特位越高,则对最终的颜色影响越大,因此可合并高位相同,而低位不同的颜色,如有11010110,11010001,则可用11010000表示这两种颜色。
八叉树顾名思义,每个节点有八个子节点,为啥是八个,因为二进制000-111共八位数,用于量化的八叉树一共有9层,根节点独占一层,rgb共八位值,每位占一层。下面详细讲解该方法的基本思想。插入颜色值(109,204,170)时,取R、G、B值的最高比特位组成011即为十进制3,插入第0层的第三个子节点,作为下一次递归的位置;进入第1层,取左第二比特位,得到值6,插入第1层的第6个子节点,第6个子节点即为下一层递归的位置。以次类推,直到找到第八层的叶子节点,叶子节点只存放颜色数量,当递归到叶子节点就把叶子节点中的uiPixelCount加1。下图为简化的演示过程,只演示几层。
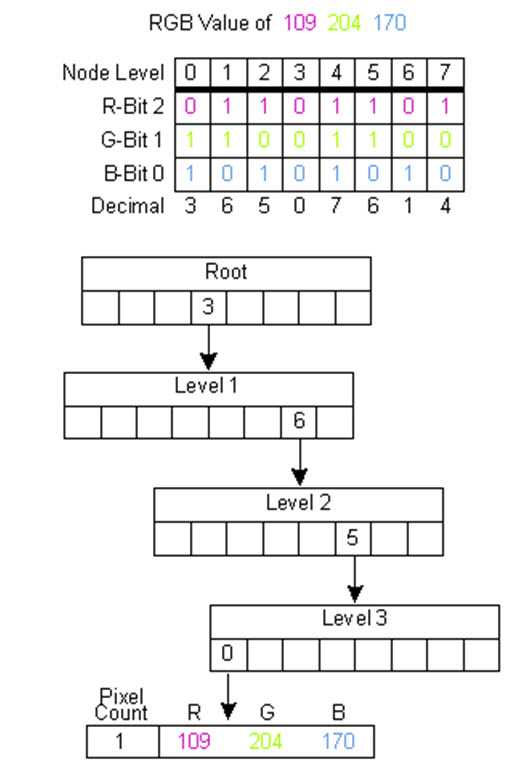
若为满8叉树,则叶子节点数量可达88,这显然失去了颜色量化的意义,因此当叶子节点超过一定的数量,则需要对叶子节点进行合并的操作,需要注意的是每次为了加快速度,每次合并的叶子节点都是当前递归到的最新节点,因此该节点可能不是表示像素数最小的节点,该操作的演示过程如下。
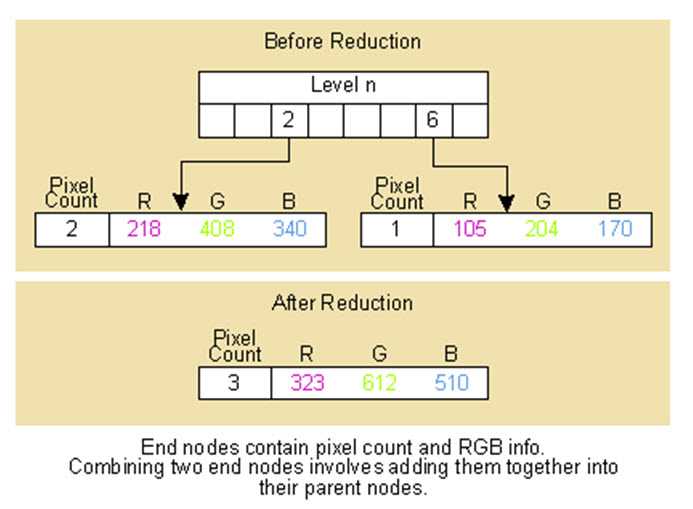
合并的基本思想是,将第n层的两个叶节点的颜色分量以及计数值相加保存在其父节点上,并裁掉这两个叶子节点,其父节点成为叶子节点。可见合并的过程是向上的过程,被剪裁掉的节点永远不会再向下生长。
八叉树虽然效果很好,但对于较大的图像来说,从整幅图像遍历得到调色板的过程还是比较耗时,在多次实验发现,从一幅图像的缩略图中得到的调色板与原图差异并不大,因此可用从原图的缩略图建立调色板,减少耗时。为进一步优化速度与量化效果,采用最邻近插值法获得缩略图,速度既快,又不引入新的颜色。
原文:https://www.cnblogs.com/chasonyu/p/11006827.html