斜率优化

简单介绍

斜率优化是一种优化dp的方法，形如单调队列，但针对的方程不同。 单调队列优化形如f[i]=max(f[j]+a[i])f[i]=max(f[j]+a[i])的方程，而斜率优化可以将形如f[i]=max(f[j]*a[i]+b[i])f[i]=max(f[j]∗a[i]+b[i])的方程从O(n^2)O(n2)优化到O(n)O(n)

做法

step1：列出暴力dp的状态转移方程

step2：将方程转移为jj比kk更优时\frac{y_j-y_k}{x_j-x_k}<a_ixj?−xk?yj?−yk??<ai?或\frac{y_j-y_k}{x_j-x_k}>a_ixj?−xk?yj?−yk??>ai?的形式

step3：\frac{y_j-y_k}{x_j-x_k}<a_ixj?−xk?yj?−yk??<ai?则维护下凸壳；\frac{y_j-y_k}{x_j-x_k}>a_ixj?−xk?yj?−yk??>ai?则维护上凸壳

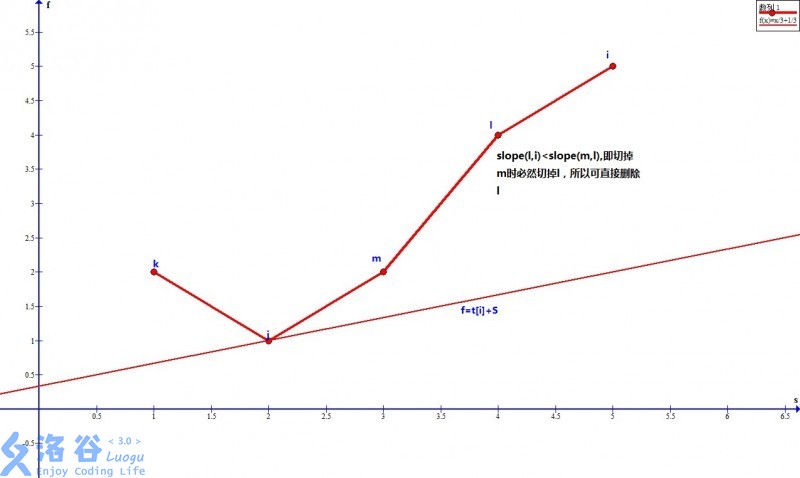
维护方法：

用直线y=a_iy=ai?切这个凸包，找出截距最大者，实现方法即为从左侧将斜率小于或大于a_iai?的点删除

插入时将插入点两侧破坏凸包性质的点删除即可

几个例题

1. P2365 任务安排

2. P4027 [NOI2007]货币兑换

3. P2120 [ZJOI2007]仓库建设

4. P3195 [HNOI2008]玩具装箱TOY

斜率优化

原文：https://www.cnblogs.com/guoshaoyang/p/10925784.html