[实变函数]4.4 依测度收敛

时间：2014-02-15 01:09:24 阅读：394 评论：0 收藏：0 [点我收藏+]

1 以前学过

点态收敛, 一致收敛,

$\bex \mbox{ 点态收敛},\quad \mbox{ 一致收敛}, \eex$

本节将用测度引进另外一种收敛概念---``依测度收敛‘‘:

(f k ? f) (菲赫金哥尔茨的记号) ? ? 误差 σ > 0, E [| f k ? f | \geq σ] 虽然可能很多, 但其测度 \to 0 (k \to \infty) .

$\beex \bea &\quad (f_k\ra f)\ (\mbox{菲赫金哥尔茨的记号})\\ &\lra \forall\mbox{ 误差 }\sigma>0,\ E[|f_k-f|\geq \sigma]\mbox{ 虽然可能很多, 但其测度 }\to 0\ (k\to\infty). \eea \eeex$

2 依测度收敛:

(f k ? f) ? ? σ > 0, lim k \to \infty m [| f k ? f | \geq σ] = 0.

$\bex (f_k\ra f)\lra \forall\ \sigma>0,\ \lim_{k\to\infty}m [|f_k-f|\geq \sigma]=0. \eex$

3 依测度收敛与 $\ae$ 收敛的区别:

(1) 依测度收敛但不收敛的例子.

(2) $\ae$ 收敛但不依测度收敛的例子:

f k (x) = {1, 0, x \in (0, n] x \in (n, + \infty) .

$\bex f_k(x)=\sedd{\ba{ll} 1,&x\in (0,n]\\ 0,&x\in (n,+\infty) \ea}. \eex$

4 依测度收敛与 $\ae$ 收敛的联系:

(1) (Riesz 定理)

(f k ? f) ? ? {k j}, s . t . f k j \to f, a . e . .

$\bex (f_k\ra f)\ra \exists\ \sed{k_j},\st f_{k_j}\to f, \ae. \eex$

证明:

f k ? f ? ? σ > 0, lim k \to \infty m [| f k ? f | \geq σ] = 0 ? ? σ > 0, ? ε > 0, ? k, s . t . m (E [| f k ? f | \geq σ]) < ε ? ? s \in Z +, ? k s, s . t . m E s < 1 2 s (E s = E [| f k s ? f | \geq 1 2 s]) ? m (\cup \infty s = 1 E s) < \sum s = 1 \infty 1 2 s = 1 < \infty ? m (lim ˉ ˉ ˉ ˉ ˉ s \to \infty E s) = 0 (Page 75 T 11) ? f k s \to f 于 E ? lim ˉ ˉ ˉ ˉ ˉ s \to \infty E s = \cup \infty m = 1 \cap \infty s = m E [| f k s ? f | < 1 2 s] .

$\beex \bea &\quad f_k\ra f\\ &\ra \forall\ \sigma>0,\ \lim_{k\to\infty}m [|f_k-f|\geq \sigma]=0\\ &\ra \forall\ \sigma>0,\ \forall\ \ve>0,\ \exists\ k,\st m(E[|f_k-f|\geq \sigma])<\ve\\ &\ra \forall\ s\in\bbZ^+,\ \exists\ k_s,\st mE_s<\frac{1}{2^s}\quad\sex{E_s=E\sez{|f_{k_s}-f|\geq \frac{1}{2^s}}}\\ &\ra m\sex{\cup_{s=1}^\infty E_s}<\sum_{s=1}^\infty \frac{1}{2^s}=1<\infty\\ &\ra m \sex{\varlimsup_{s\to\infty}E_s}=0\quad\sex{\mbox{Page 75 T 11}}\\ &\ra f_{k_s}\to f\mbox{ 于 }E\bs \varlimsup_{s\to\infty}E_s=\cup_{m=1}^\infty \cap_{s=m}^\infty E\sez{|f_{k_s}-f|<\frac{1}{2^s}}. \eea \eeex$

(2) (Lebesgue) 设 $mE<\infty$ ,

a . e . 有限的可测函数列 {f k} a . e . 收敛于 a . e . 有限的函数 f .

$\bex \ae\mbox{ 有限的可测函数列 }\sed{f_k}\ae \mbox{ 收敛于 }\ae\mbox{ 有限的函数 }f. \eex$ 则

f k ? f .

$\bex f_k\ra f. \eex$

证明:

m (\cup \infty j = 1 \cap \infty N = 1 \cup \infty k = N E [| f k ? f | \geq 1 j]) = 0 ? ? j \in Z +, lim N \to \infty m (\cup \infty k = N E [| f k ? f | \geq 1 j]) = 0 ? ? j \in Z +, lim N \to \infty m (E [| f N ? f | \geq 1 j]) = 0.

$\beex \bea &\quad m\sex{\cup_{j=1}^\infty \cap_{N=1}^\infty \cup_{k=N}^\infty E\sez{|f_k-f|\geq \frac{1}{j}}}=0\\ &\ra \forall\ j\in\bbZ^+,\ \lim_{N\to\infty} m\sex{\cup_{k=N}^\infty E\sez{|f_k-f|\geq \frac{1}{j}}}=0\\ &\ra \forall\ j\in\bbZ^+,\ \lim_{N\to\infty} m\sex{E\sez{|f_N-f|\geq \frac{1}{j}}}=0. \eea \eeex$ 注: Lebesgue 定理中

mE<∞

$mE<\infty$ 是必须的. 否则有反例:

f k (x) = {1, 0, x \in (0, n] x \in (n, + \infty) .

$\bex f_k(x)=\sedd{\ba{ll} 1,&x\in (0,n]\\ 0,&x\in (n,+\infty) \ea}. \eex$

5 依测度收敛的极限的唯一性 (在 $\ae$ 意义下):

(f k ? f, f k ? g) ? f = g, a . e . .

$\bex (f_k\ra f,\ f_k\ra g)\ra f=g,\ae. \eex$ 证明:

E [| f ? g | > 0] = \cup \infty j = 1 E [| f ? g | \geq 1 j] = \cup \infty j = 1 E [| (f k ? f) ? (f k ? g) | \geq 1 j] ? \cup \infty j = 1 (E [| f k ? f | \geq 1 2 j] \cup E [| f k ? g | \geq 1 2 j]) .

$\beex \bea E[|f-g|>0] &=\cup_{j=1}^\infty E\sez{|f-g|\geq\frac{1}{j}}\\ &=\cup_{j=1}^\infty E\sez{|(f_k-f)-(f_k-g)|\geq \frac{1}{j}}\\ &\subset \cup_{j=1}^\infty \sex{E\sez{|f_k-f|\geq\frac{1}{2j}} \cup E\sez{|f_k-g|\geq\frac{1}{2j}}}. \eea \eeex$

6 各种收敛态的关系总结:

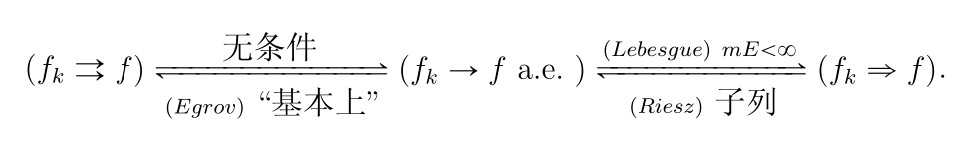
bubuko.com,布布扣

7 作业: Page 95, T 15.

[实变函数]4.4 依测度收敛

原文：http://www.cnblogs.com/zhangzujin/p/3549165.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)