数据机构按照其逻辑结构可分为线性结构、树结构、图结构
列表(其它语言是数组)是一种基本数据类型。
关于列表问题:
1、列表的元素是如何存储的?(存内存地址(64位机器固定8bytes))
2、如何查找元素?(从列表起始位置的内存地址,查第几个元素就起始位置加n*8)
3、列表不用显示声明长度?(python内部通过完整拷贝来调整列表长度)
栈(Stack)是一个数据集合,可以理解为只能在一端进行插入或删除操作的列表。
栈的特点:后进先出 LIFO
栈的概念:栈顶,栈底
栈的基本操作:
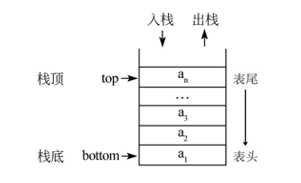
栈的实现
使用一般的列表即可实现栈
class Stack: def __init__(self): self.stack = [] def push(self, data): self.stack.append(data) def pop(self): return self.stack.pop() def get_top(self): if len(self.stack) > 0: return self.stack[-1] else: return None def is_empty(self): return len(self.stack) > 0
栈的应用 -- 括号匹配问题
括号匹配问题:给一个字符串,其中包括小括号、中括号、大括号,求该字符串中的括号是否匹配。
例如:

def brace_match(s): match = {‘}‘: ‘{‘, ‘]‘: ‘[‘, ‘)‘: ‘(‘} stack = Stack() for ch in s: if ch in {‘(‘, ‘[‘, ‘{‘}: stack.push(ch) else: # ch in {‘}‘,‘]‘,‘)‘} if stack.is_empty(): return False elif stack.get_top() == match[ch]: stack.pop() else: return False if stack.is_empty(): return True else: return False print(brace_match(‘[{()}(){()}[]({}){}]‘)) print(brace_match(‘[]}‘))
队列(queue)是一个数据集合,仅允许在列表的一端进行插入,另一端进行删除。
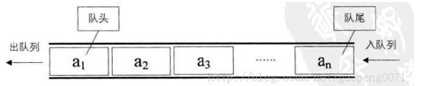
队列的实现
初步设想:列表+两个下标指针
创建一个列表和两个变量,front变量指向队首,rear变量指向队尾。初始时,front和rear都为0
进队操作:元素写到li[rear]的位置,rear自增1
出队操作:返回li[front]的元素,front自增1

出现d的情况后,队列无法继续添加元素,但是列表里面有位置是空的,这一点非常不好
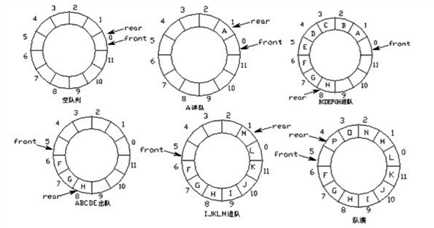
队列的实现原理 -- 环形队列
环形队列:当队尾指针front == Maxsize + 1时,再前进一个位置就自动到0
实现方式:求余运算
队首指针前进1:front = (front+1) % maxsize
队尾指针前进1:rear = (rear+1) % maxsize
队空条件:rear == front队满条件:(rear+1)% maxsize == front

class Queue: def __init__(self, size=100): self.queue = [0 for i in range(size)] self.size = size self.rear = 0 # 队尾指针 self.front = 0 # 队首指针 def push(self, element): if not self.is_filled(): self.rear = (self.rear + 1) % self.size self.queue[self.rear] = element else: raise IndexError("Queue is filled.") def pop(self): if not self.is_empty(): self.front = (self.front + 1) % self.size return self.queue[self.front] else: raise IndexError("Queue is empty.") # 判断队空 def is_empty(self): return self.rear == self.front # 判断队满 def is_filled(self): return (self.rear + 1) % self.size == self.front q = Queue(5) for i in range(4): q.push(i) print(q.pop()) q.push(4)
队列的内置模块
使用方法:from collections import deque
创建队列:queue = deque(li)
进队:append
出队:popleft
双向队列队首进队:appendleft
双向队列队尾进队:pop
栈和队列的应用 -- 迷宫问题

解决方法1:栈--深度优先搜索(回溯法)
思路:从一个节点开始,任意找下一个能走的点,当找不到能走的点时,退回上一个点寻找是否有其他方向的点。
(使用栈存储当前路径)
原文:https://www.cnblogs.com/Xuuuuuu/p/10846124.html