优先队列至少满足插入元素和删除最小者(或最大者)的这两种操作。它相比于查找树少了许多如查找、排序等基本操作。
一.二叉堆
利用数组实现模拟树的结构,使其可以以 O(logN)的时间完成最坏情况下优先队列所支持的两种基本操作。
对于二叉堆(最小元素在根部的堆)的插入操作,即将新的元素添加到数组的末尾,并通过上滤使其交换到正确的位置。
同样,对于其的删除最小元素的操作,即将堆的最后一个元素覆盖代替根部元素,再通过下滤操作使其交换回正确的位置。
二叉堆的插入操作代码实现如下,
void insert( Comparable && x) { if (currentSize == Array.size() - 1) Array.resize(Array.size() * 2); int hole = ++currentSize; Array[0] = std::move(copy); //对插入元素进行上滤,使其交换到正确位置上 for (; hole>1&&x < Array[hole / 2]; hole /= 2) Array[hole] = std::move(Array[hole / 2]); Array[hole] = std::move(x); }
实现中,代码使用覆盖的形式进行,以减少交换元素中带来的额外开销,提高了程序的效率。同样,再其的删除元素的操作实现中,也进行元素的覆盖,提高程序的效率。
二叉堆的删除操作代码实现如下,
void deleteMin() { if (isEmpty()) throw UnderflowException{}; Array[1] = std::move(Array[currentSize--]); percolateDown(1); } void deleteMin(Comparable & minItem) { if (isEmpty()) throw UnderflowException{}; minItem = std::move(Array[1]); Array[1] = std::move(Array[currentSize--]); percolateDown(1); } void buildHeap() { for (int i = currentSize / 2; i > 0; --i) percolateDown(i); } void percolateDown(int hole) { int child; Comparable tmp = std::move(Array[hole]); for (; hole * 2 <= currentSize; hole = child) { child = hole * 2; //先确定是左右孩子的存在与大小 if (child != currentSize && Array[child + 1] < Array[child]) ++child; //再确定是否进行交换 if (Array[child] < tmp) Array[hole] = std::move(Array[child]); else break; } Array[hole] = std::move(tmp); }
二.左式堆
同样有二叉堆的结构性和有序性,但左式堆不是一种理想平衡树,不过其支持两个不同的左式堆以O(N)时间进行合并操作,相对以数组实现的二叉堆,二叉堆可能需要以O(NlogN)时间进行合并。
在左式堆中,每一个节点的左儿子零路径长要大于等于右儿子零路径长。且有定理:有r个节点在左式堆的右路径上,则该堆至少有2r-1个节点。
而由该定理可得,有N个节点的左式堆,其有一条最多含 个节点的右路径。
个节点的右路径。
左式堆的基本操作也是插入新元素和删除最小者,但这两操作中都用到了更基本的操作--合并。
合并的操作,首先需要判断合并的两个堆H1和H2(单元素的也可构建一个堆)是否为空,若为空,则返回另一者。若两个堆非空,则判断这两个堆根元素的大小,选取具有较小根元素的为基本堆。
假设H1为基本堆,若基本堆H1的左子树堆为空,则其左子树堆直接接上H2。若非空,则基本堆H1的右子树堆为右子树堆和H2 堆的重新合并(即重新调用合并,将H1的右子树堆和H2进行合并)。在子合并退出前,比较基本堆H1的左儿子零路径长是否大于等于右儿子零路径长,否则进行交换,并且修改基本堆的零路径长信息为其右儿子零路径长加1,最后返回基本堆H1。
合并基本流程的操作代码如下,
LeftistNode * merge(LeftistNode *h1, LeftistNode * h2) { if (h1 == nullptr) return h2; if (h2 == nullptr) return h1; //两个合并树堆非空,选择有较小元素的基本堆进行合并 if (h1->element < h2->element) return merge1(h1, h2); else { return merge1(h2, h1); } } LeftistNode * merge1(LeftistNode *h1, LeftistNode * h2) { if (h1->left == nullptr) h1->left = h2; else { //基本堆的右子树堆非空,调用 merge(h1->right ,h2) h1->right = merge(h1->right, h2); if (h1->left->npl < h1->right->npl) swapChildren(h1); h1->npl = h1->right->npl + 1; } return h1; }
三.二项队列
二项队列适用于插入频繁,而删除操作需求较少的数据对象。因为,二项队列的插入操作只需花费平均的常数时间,而删除最小者需要的时间为O(logN)。
二项队列由一组高度互不相同的二项树组成,而一棵高度为k的二项树Bk由一棵二项树Bk-1附接到另一棵Bk-1的根上构成。如下图
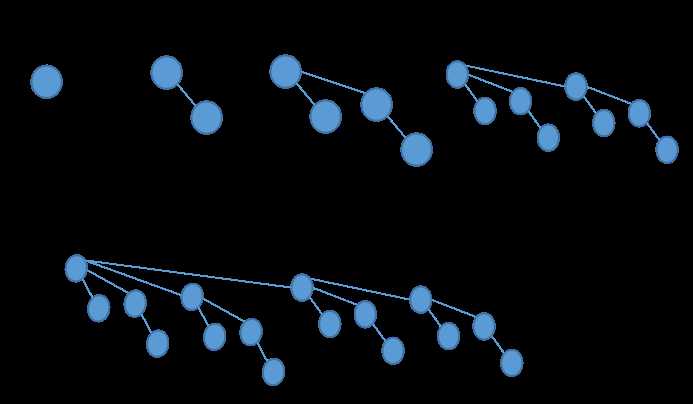
可见,高度为k的二项树刚好有2K个节点,而一个有N个元素的二项队列则最多有O(logN)棵不同的二项树。
二项队列支持插入,删除最小者的操作,同二叉堆一样,这两种操作也是基于合并的基本操作。
其合并基本流程的操作代码如下,
void merge(binomialQueue & rhs) { if (this == &rhs) return; currentSize += rhs.currentSize; if (currentSize > capacity()) //合并元素个数大于容量,需扩容 { int oldNumTrees = theTrees.size(); int newNumTrees = max(theTrees.size(), rhs.theTrees.size()) + 1; theTrees.resize(newNumTrees); for (int i= oldNumTrees; i < newNumTrees; ++i) theTrees[i] = nullptr; } BinomialNode *carry = nullptr; for (int i = 0, j = 1; j <= currentSize; ++i, j *= 2) { BinomialNode *t1 = theTrees[i]; BinomialNode *t2 = (i < rhs.theTrees.size() ? rhs.theTrees[i] : nullptr); int whichCase = (t1 == nullptr ? 0 : 1); whichCase += (t2 == nullptr ? 0 : 2); whichCase += (carry == nullptr ? 0 : 4); switch (whichCase) { case 0: //都为空 case 1: // 只有 t1 不空 break; case 2: //只有 t2 不空 theTrees[i] = t2; rhs.theTrees[i] = nullptr; break; case 4: //只有 carry 不空 theTrees[i] = carry; carry = nullptr; break; case 3: //t1 和 t2 不空 carry = combineTrees(t1, t2); theTrees[i] = rhs.theTrees[i] = nullptr; break; case 5: //t1 和 carry 不空 carry = combineTrees(t1, carry); theTrees[i] = nullptr; break; case 6: //t2 和 carry 不空 carry = combineTrees(t2, carry); rhs.theTrees[i] = nullptr; break; case 7: //三者都不空 theTrees[i] = carry; carry = combineTrees(t1, t2); rhs.theTrees[i] = nullptr; break; } } for (auto & root : rhs.theTrees) root = nullptr; rhs.currentSize = 0; }
二项队列利用二项树树根组成的数组实现,数组的下标代表了二项树的高度。两个二项队列进行合并,与加法进位相似,可能会向前产生一棵二项树,根据两个二项队列在i的位置是否有二项树以及在前面的合并中是否有产生二项树的情况(依据排列组合有8种情况),选择不同的二项树合并方式。
在二项队列删除最小者的操作中,需要将最小者位置上的二项树分裂成一个二项队列,再将这队列与原来的二项队列(需要将最小者位置置空)进行合并。其操作代码如下
void deleteMin() { Comparable x; deleteMin(x); } void deleteMin(const Comparable &minItem) { if (isEmpty()) throw UnderflowException{}; int minIndex = findMinIndex(); minItem = theTrees[minIndex]->element; BinomialNode * oldRoot = theTrees[minIndex]; BinomialNode * deletedTree = oldRoot->leftChild; delete oldRoot; //最小者位置上的二项树分裂形成新的二项队列 binomialQueue deletedQueue; deletedQueue.theTrees.resize(minIndex + 1); deletedQueue.currentSize = (1 << minIndex) - 1; for (int j = minIndex - 1; j >= 0; --j) { deletedQueue.theTrees[j] = deletedTree; deletedTree = deletedTree->nextSibling; deletedQueue.theTrees[j]->nextSibling = nullptr; } //将原二项队列的最小者位置置空 theTrees[minIndex] = nullptr; currentSize -= deletedQueue.currentSize + 1; //合并这两个二项队列 merge(deletedQueue); }
原文:https://www.cnblogs.com/lincz/p/10847268.html