①公式

此处用高斯核函数计算样本x和标记向量之间的相似度，公式：

②分情况讨论

 ③图像

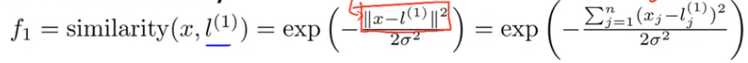
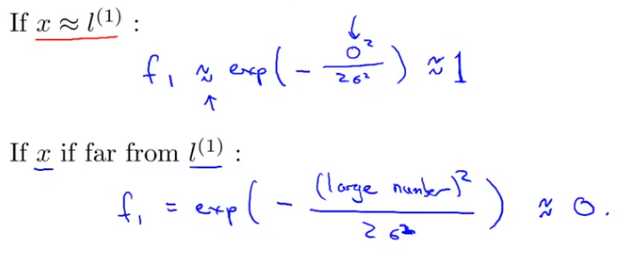
 当变化时，假定已知一个标记向量，则在空间坐标系中，核函数的图像是这样变化的：

④作用

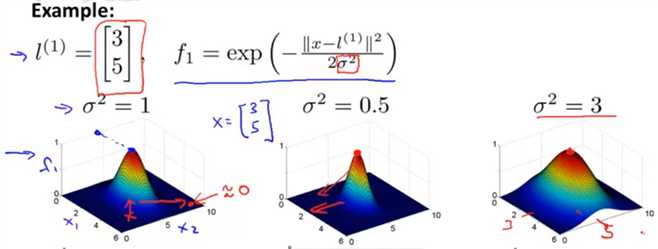
给定n个标记向量，通过核函数利用样本分别和这n个标记向量进行计算，可以生成如下n个特征变量

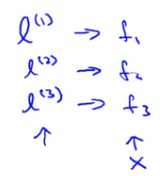
通过这些个特征变量并通过某个算法学习到θ的值，以样本的特征为坐标，就可以画出更加复杂的决策边界：

⑤标记点的选择

若有m个样本，可以把这m个样本就设定为m个标记点。即：

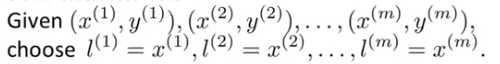
特征变量f是x1,x2,x3...的函数，对于第i个样本，可以计算它对应的特征变量f，此时对于每个样本就对应一组特征变量f：

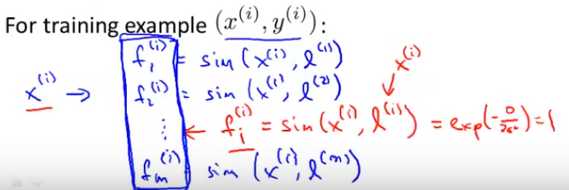
若再已知θ就可以进行预测了：

 ⑥SVM代价函数（考虑核函数）

 ⑦参数过大或过小

高斯核函数

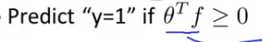
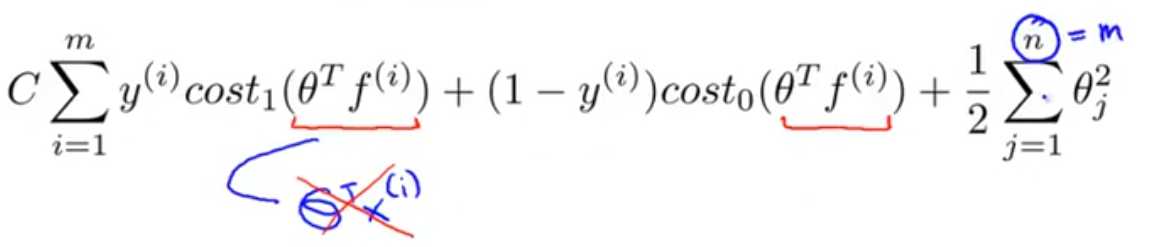
原文：https://www.cnblogs.com/pjishu/p/10816716.html