初学树

时间：2019-05-01 15:32:21 阅读：115 评论：0 收藏：0 [点我收藏+]

现在来说说树。树的图结构可以使我们明白树具体是什么样子，但是存储时并不需要理会。

1、树是一种非线性的数据结构，但是我们常用线性结构来存放一棵树。

主要分以下两种：

（1）对于二叉树：

1 typedef struct{
2     int lch;
3     int rch;
4 }node;
5 
6 int node[10];

View Code

定义一个节点，然后采用结构体数组来依次存放。

（2）非二叉树：

1 typedef struct{
2     int *next;
3 }node;

View Code

将当前节点的孩子用一个指针指向，可以根据需要申请合适的空间。

2、学习例题的一些想法

（1）题目：

给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而右边的就不是同构的。

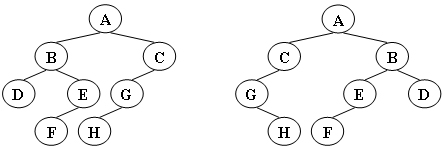
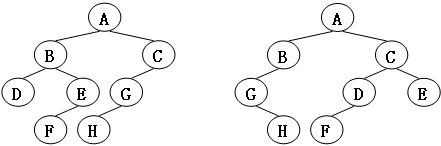
现给定两棵树，请你判断它们是否是同构的。

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

解决代码：

  1 #include <iostream>
  2 #include <queue>
  3 using namespace std;
  4 
  5 //节点定义 
  6 typedef struct{
  7     char name;
  8     int lch;
  9     int rch;
 10 }node;
 11 
 12 //函数原型声明
 13 void init(node []);
 14 int bulidTree(node []);
 15 int searchTreeB(char, node []);
 16 void compareTree(node [], int, node [], int);
 17 bool compareNode(char, char, char, char);
 18 
 19 
 20 int main()
 21 {
 22     node treeA[11], treeB[11];
 23     int rootA, rootB;
 24 
 25 //    建立树，并找根节点 
 26     rootA = bulidTree(treeA);
 27     rootB = bulidTree(treeB);
 28 
 29 //    比较树 
 30     compareTree(treeA, rootA, treeB, rootB);
 31 
 32     return 0;
 33 }
 34 
 35 //初始化0下标 
 36 void init(node t[])
 37 {
 38     t[0].name = ‘ ‘;
 39     t[0].lch = 0;
 40     t[0].rch = 0;
 41 }
 42 
 43 //建立树 
 44 int bulidTree(node t[])
 45 {
 46     bool check[11] = {false};
 47     int n;
 48     char x, y;
 49     
 50     cin >> n;
 51     if(n == 0)
 52     {
 53         return -1;    //节点个数为0，空树，根节点为-1； 
 54     }
 55     
 56 //    非空树，将0下标代替没有孩子节点的-1，以免越界读 
 57     n++;
 58     init(t);    //初始化0下标 
 59     
 60 //    从1下标开始输入，孩子节点下标+1 
 61     for (int i=1; i<n; i++)
 62     {        
 63         cin >> t[i].name >> x >> y;
 64         
 65         if(x != ‘-‘)
 66         {
 67           t[i].lch = x - ‘0‘ + 1;
 68           check[t[i].lch] = true;
 69         }
 70         else t[i].lch = 0;
 71           
 72         if(y != ‘-‘)
 73         {
 74           t[i].rch = y - ‘0‘ + 1;
 75           check[t[i].rch] = true;
 76         }
 77         else t[i].rch = 0;
 78     }
 79     
 80 //    找根节点 
 81     for (int i=1; i<n; i++){
 82         if(!check[i]) return i;
 83     }
 84 }
 85 
 86 //根据当前出队的treeA的name寻找其在treeB中的下标 
 87 int searchTreeB(char ch, node treeB[])
 88 {
 89     int i;
 90     
 91     for(i=1; i<11; i++)
 92     {
 93         if(ch == treeB[i].name)
 94         {
 95             return i;    //找到，返回下标 
 96         }
 97     }
 98     
 99     if(i == 11) return 0;    //寻找失败，返回0 
100 }
101 
102 //比较两棵树是否为同构 
103 void compareTree(node treeA[], int rootA, node treeB[], int rootB)
104 {
105     int tmp;
106     queue<int> q;    //队列操作 
107     q.push(rootA); //根结点所在下标入栈
108     int B;    //存放searchTreeB函数调用的结果
109     
110 //    空树 
111     if(rootA == -1 && rootB == -1)
112     {
113         cout << "Yes";
114         return;
115     }
116     
117 //    非空树 
118     while(!q.empty())
119     {
120         tmp = q.front(); 
121         q.pop();
122         if(tmp!=0)
123         {
124 //            查询当前treeA的节点name在treeB中的下标 ，不存在则退出 
125             B = searchTreeB(treeA[tmp].name, treeB);
126             if(B == 0)
127             {
128                 cout << "No";
129                 return;
130             }
131             
132 //            存在则比较各自的左右孩子name是否相同，不同则退出 
133             if(!compareNode(treeA[treeA[tmp].lch].name, treeA[treeA[tmp].rch].name, treeB[treeB[B].lch].name, treeB[treeB[B].rch].name))
134             {
135                 cout << "No";
136                 return;
137             }
138             q.push(treeA[tmp].lch);
139             q.push(treeA[tmp].rch);
140         }
141     }
142     cout << "Yes"; 
143 }
144 
145 //比较节点的孩子是否相同 
146 bool compareNode(char Al, char Ar, char Bl, char Br)
147 {
148     if((Al==Bl || Al==Br) && (Ar==Bl || Ar==Br))
149         return true;
150     else return false;
151 }

View Code

解决思路：我的想法是：按照定义，如果是同构树，则第一棵树的任一节点都可以在第二颗树找到，并且第一棵树的节点的左孩子==第二颗树的节点的左孩子/右孩子 && 第一棵树的节点的右孩子==第二颗树的节点的左孩子/右孩子。即以下代码（完整代码的123-126行和146-151行）：

 1 if(!compareNode(treeA[treeA[tmp].lch].name, treeA[treeA[tmp].rch].name, treeB[treeB[B].lch].name, treeB[treeB[B].rch].name))
 2             {
 3                 cout << "No";
 4                 return;
 5             }
 6 
 7 
 8 
 9 //比较节点的孩子是否相同 
10 bool compareNode(char Al, char Ar, char Bl, char Br)
11 {
12     if((Al==Bl || Al==Br) && (Ar==Bl || Ar==Br))
13         return true;
14     else return false;
15 }

View Code

出现的问题：原本的代码：如果节点的孩子节点没有，则将孩子节点的下标置为 -1 ，然后在比较是就会发生越界读的问题。看代码：

1  if(!((treeA[treeA[tmp].lch].name==treeB[treeB[B].lch].name || treeA[treeA[tmp].lch].name==treeB[treeB[B].rch].name) && (treeA[treeA[tmp].rch].name==treeB[treeB[B].lch].name || treeA[treeA[tmp].rch].name==treeB[treeB[B].rch].name)))
2             {
3                 cout << "No";
4                 return;
5             }

View Code

如果如上边的左图，则在比较节点 C 时，就会比较 G== treeB[-1].name 。

解决问题：因为发生了越界读，那么把他越界的地方包含进来就好。所以在遇到孩子节点没有时，不在将下标置为 -1 ，而是改为 0 ，将结构体数组的0下标作为没有孩子节点的下标，避免越界读。（代码的60-78行）

  1 #include <iostream>
  2 #include <queue>
  3 using namespace std;
  4 
  5 //节点定义 
  6 typedef struct{
  7     char name;
  8     int lch;
  9     int rch;
 10 }node;
 11 
 12 //函数原型声明
 13 void init(node []);
 14 int bulidTree(node []);
 15 int searchTreeB(char, node []);
 16 void compareTree(node [], int, node [], int);
 17 bool compareNode(char, char, char, char);
 18 
 19 
 20 int main()
 21 {
 22     node treeA[11], treeB[11];
 23     int rootA, rootB;
 24 
 25 //    建立树，并找根节点 
 26     rootA = bulidTree(treeA);
 27     rootB = bulidTree(treeB);
 28 
 29 //    比较树 
 30     compareTree(treeA, rootA, treeB, rootB);
 31 
 32     return 0;
 33 }
 34 
 35 //初始化0下标 
 36 void init(node t[])
 37 {
 38     t[0].name = ‘ ‘;
 39     t[0].lch = 0;
 40     t[0].rch = 0;
 41 }
 42 
 43 //建立树 
 44 int bulidTree(node t[])
 45 {
 46     bool check[11] = {false};
 47     int n;
 48     char x, y;
 49     
 50     cin >> n;
 51     if(n == 0)
 52     {
 53         return -1;    //节点个数为0，空树，根节点为-1； 
 54     }
 55     
 56 //    非空树，将0下标代替没有孩子节点的-1，以免越界读 
 57     n++;
 58     init(t);    //初始化0下标 
 59     
 60 //    从1下标开始输入，孩子节点下标+1 
 61     for (int i=1; i<n; i++)
 62     {        
 63         cin >> t[i].name >> x >> y;
 64         
 65         if(x != ‘-‘)
 66         {
 67           t[i].lch = x - ‘0‘ + 1;
 68           check[t[i].lch] = true;
 69         }
 70         else t[i].lch = 0;
 71           
 72         if(y != ‘-‘)
 73         {
 74           t[i].rch = y - ‘0‘ + 1;
 75           check[t[i].rch] = true;
 76         }
 77         else t[i].rch = 0;
 78     }
 79     
 80 //    找根节点 
 81     for (int i=1; i<n; i++){
 82         if(!check[i]) return i;
 83     }
 84 }
 85 
 86 //根据当前出队的treeA的name寻找其在treeB中的下标 
 87 int searchTreeB(char ch, node treeB[])
 88 {
 89     int i;
 90     
 91     for(i=1; i<11; i++)
 92     {
 93         if(ch == treeB[i].name)
 94         {
 95             return i;    //找到，返回下标 
 96         }
 97     }
 98     
 99     if(i == 11) return 0;    //寻找失败，返回0 
100 }
101 
102 //比较两棵树是否为同构 
103 void compareTree(node treeA[], int rootA, node treeB[], int rootB)
104 {
105     int tmp;
106     queue<int> q;    //队列操作 
107     q.push(rootA); //根结点所在下标入栈
108     int B;    //存放searchTreeB函数调用的结果
109     
110 //    空树 
111     if(rootA == -1 && rootB == -1)
112     {
113         cout << "Yes";
114         return;
115     }
116     
117 //    非空树 
118     while(!q.empty())
119     {
120         tmp = q.front(); 
121         q.pop();
122         if(tmp!=0)
123         {
124 //            查询当前treeA的节点name在treeB中的下标 ，不存在则退出 
125             B = searchTreeB(treeA[tmp].name, treeB);
126             if(B == 0)
127             {
128                 cout << "No";
129                 return;
130             }
131             
132 //            存在则比较各自的左右孩子name是否相同，不同则退出 
133             if(!compareNode(treeA[treeA[tmp].lch].name, treeA[treeA[tmp].rch].name, treeB[treeB[B].lch].name, treeB[treeB[B].rch].name))
134             {
135                 cout << "No";
136                 return;
137             }
138             q.push(treeA[tmp].lch);
139             q.push(treeA[tmp].rch);
140         }
141     }
142     cout << "Yes"; 
143 }
144 
145 //比较节点的孩子是否相同 
146 bool compareNode(char Al, char Ar, char Bl, char Br)
147 {
148     if((Al==Bl || Al==Br) && (Ar==Bl || Ar==Br))
149         return true;
150     else return false;
151 }

View Code

初学树

原文：https://www.cnblogs.com/ZwQuan/p/10799859.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)