简单数据结构：
一、二叉搜索树
1、前置技能：
n/1+n/2+……+n/n=O(n log n） （本天复杂度常涉及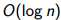
）
2、入门题引入：
N<=100000.
这里多了一个删除的操作，因此要将所有的数都记录下来维护。一个个枚举很容易超时，这时就到了二叉搜索树显示本领的时候了。
（注：子树节点的key值小/大于这个点，即子树中所有的节点的key值都小/大于这个点。同时不考虑有两个节点key值相等的情况）
实例：
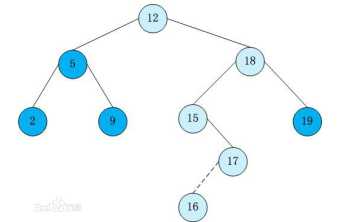
1、查询最大/小值：
最大值自然就是往右儿子走啦。
核心代码（最小值）：
1 int FindMin() 2 { 3 int x=root; 4 while(ls[x]) x=ls[x]; 5 return key[x]; 6 }
2、插入一个值：
核心代码：
1 void insert(int val) { 2 key[+ + tot] = val; 3 ls[tot] = rs[tot] = 0; 4 int now = root;//当前访问的节点为now. 5 for(; ;) { 6 if (val < key[now]) 7 if (!ls[now]) ls[now] = x, fa[x] = now, break; 8 else now =ls[now]; 9 else if (!rs[now]) rs[now] = x, fa[x] =now, break; 10 else now = rs[now]; 11 } 12 }
3、删除一个值
代码：
1 int Find(int x) 2 { 3 int now = root; 4 while(key[now]! = x) 5 if (key[now] < x) now = rs[now]; else now = ls[now]; 6 return now; 7 }
设y是x右子树中所有点里，权值最小的点，则y必没有左儿子。找这个点可以从x先走一下右儿子，再走一下左儿子。找到y后，把y的右子树接到y的父节点上（必为其左子树），再用y覆盖掉x就行了。
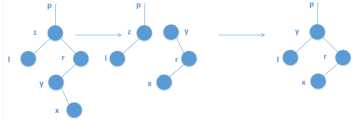
代码：
//(由于不需要求每个节点的子树大小，在相应的代码前打上的注释号） void del(int x)//删除一个值为x的点 { int id=Find(x),t=fa[id];//找到这个点的编号 if (!ls[id]&&!rs[id]) { if (ls[t]==id) ls[t]=0; else rs[t]=0; //去掉儿子边 // for (i=id;i;i=fa[i]) size[i]--; } else if (!ls[id]||!rs[id]) { int child=ls[id]+rs[id];//找存在的儿子的编号 if (ls[t]==id) ls[t]=child; else rs[t]=child; fa[child]=t;//让父亲认自己儿子为儿子，自己受到冷淡 // for (i=id;i;i=fa[i]) size[i]--; } else { int y=rs[id]; while (ls[y]) y=ls[y]; //找y if (rs[id]==y) //y正好是这个点的右儿子，则直接替代它（篡位…） { if (ls[t]==id) ls[t]=y; else rs[t]=y; fa[y]=t; ls[y]=ls[id]; fa[ls[id]]=y; // for (i=id;i;i=fa[i]) size[i]--; // size[y]=size[ls[y]]+size[rs[y]];//y的子树大小需要更新 } else //最复杂的情况 { // for (i=fa[y];i;i=fa[i]) size[i]--;//注意到变换完之后y到root路径上每个点的size都减少了1 int tt=fa[y]; //先把y提出来 ls[tt]=rs[y]; fa[rs[y]]=tt; //再来提出x if (ls[t]==x) { ls[t]=y; fa[y]=t; ls[y]=ls[id]; rs[y]=rs[id]; } else { rs[t]=y; fa[y]=t; ls[y]=ls[id]; rs[y]=rs[id]; } // size[y]=size[ls[y]]+size[rs[y]]+1;//更新一下size } } }
（这么长的代码吓我一跳）
4、
（注：子树长度包括该子树的根）
代码：
1 int Findkth(int now, int k)//当前根节点 “第k大”的k 2 { 3 if (size[rs[now]] >= k) //第k大在右子树 4 return Findkth(rs[now], k); 5 else 6 if (size[rs[now]] + 1 == k) //当前即为第k大 7 return key[now]; 8 else //第k大在左子树，由于递归后要不受递归前右子树的影响，递归进去的k进去时对递归前的整体而言，进去后只对递归后的整体而言， 9 //因此k应减去递归前右子树和根节点的数目 10 return Findkth(ls[now], k - size[rs[now]] - 1); 11 }
5、遍历：
代码：
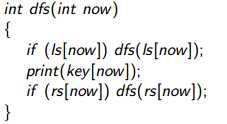
让我们回到最初的题。
一个良好的例子（数据）:3 1 2 4 5（3层深的树）
一个糟糕的例子（数据）:1 2 3 4 5（5层深的树）
二叉搜索树每次操作访问O(h)个节点。
（故建树时可先sort一遍，以中间点为根，这样深度基本就位logn级别的了）
二、二叉堆
https://www.cnblogs.com/InductiveSorting-QYF/p/10776293.html（曾经写过，安利一下，在这里就只写写新东西吧）
堆没有二叉搜索树的性质，即左边的不一定比右边的小。堆只满足儿子与父亲的关系，因此常常用来搞最大/最小值。
1、建堆：
除了一个个插入以外，还有一个时间复杂度相差不大（稍慢一点）、很便捷的方法：直接sort排下序。
2、查询最大/最小值：大/小根堆的堆顶就是啦。
3、插入删除：详见链接。
4、修改一个点的权值（以小根堆为例）：变小往上浮，变大往最小的儿子的方向下潜（交换）
应用：堆排序（详见链接）
例题：
1、丑数
题解：
考虑构造小根堆。
EX:
(注：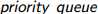
：优先队列，跟堆差不多。默认大根堆，改成小根堆一是可以重载小于号成大于号的功能（感觉怪怪的），而是在定义的类型后加上“vector<类型>，greater<类型> ”（注意最后有空格，否则右移运算符警告））
Q.push(x)插入一个元素
Q.top()访问堆顶
Q.pop()删除一个
Q.clear() 清空
深入学习：https://blog.csdn.net/byn12345/article/details/79523516
浅谈：set可看做集合，内部实际上采用红黑树。有两个特点：1、自动排序。2、每个元素只会出现一次（即没有值相等的两个元素出现在同一个set中）
功能函数：
.insert(x) ,向容器插入元素x
.erase(x) ,删除容器中的元素x
.begin() ,返回set容器第一个元素的迭代器
.end() ,返回一个指向当前set末尾元素的下一位置的迭代器.
.clear() ,删除set容器中的所有的元素
.empty() ,判断set容器是否为空
.max_size() ,返回set容器可能包含的元素最大个数(set的最大容量）
.size() ,返回当前set容器中的元素个数
.find() ,
注:访问set容器中的元素应在指向该元素的迭代器前加“*”（星号）
声明迭代器： set<类型>::iterator 名字; 注：迭代器只支持++和--两种运算。
原文：https://www.cnblogs.com/InductiveSorting-QYF/p/10792759.html