时间膨胀和长度收缩证明

狭义相对论两个基本假设：

1. 物理规律的协变性，即不同惯性系下都有
   

   \(s = v \cdot t\)

2. 光速恒定

下面用这两个假定推出时间膨胀和长度收缩

时间膨胀

假设在速度为u的火车上安装了两面镜子，分别安装在车顶和车底。从车底的镜子发出一道光到车顶，再反射回原处。问这过程用了多长时间。

假设车高\(h\), \(c\)为光速。

在车上的人看来一共花费 \(T' = 2h/c\)

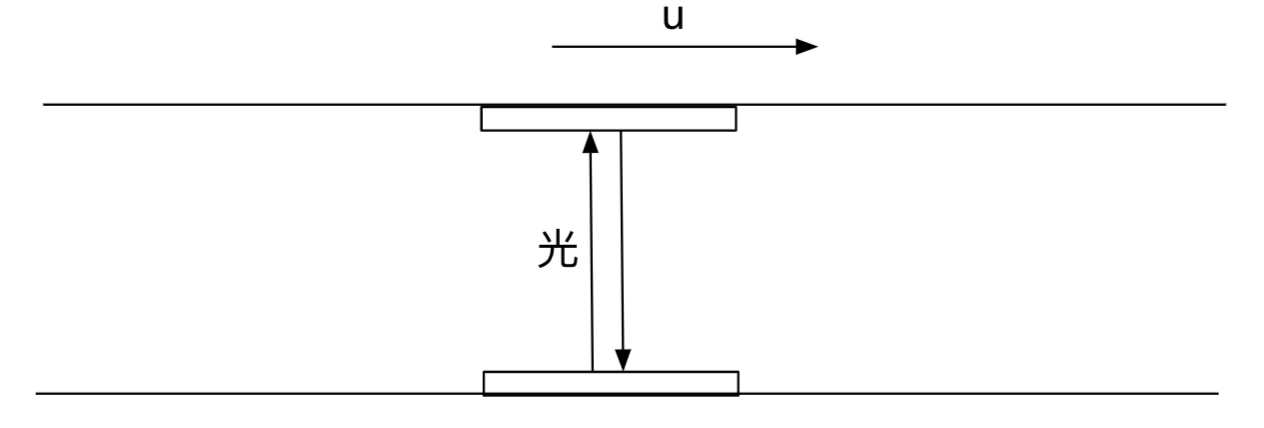
在站台上的人看来，光走了一个折线，光在垂直方向上的速度分量是 \(\sqrt{c^2 - u^2}\)， 因此\(T = 2h/\sqrt{c^2 - u^2}\)

这样，在站台上的人看来，车上的光线需要更多时间回到原处，时间变慢了：\(T = \frac{T'}{\sqrt{1 - (u/c)^2}}\)

长度收缩

现在在车头和车尾安装两面镜子，从车尾发出一束光，经车头镜子反射后回到原处。问这个过程用了多长时间。

在车上的人看来，假设车子长度为\(L'\)，则一共需要\(T' =2 L'/c\)

在站台上的人看来，假设车子长度为\(L\), 反射前，光到达车头需要

\(T_1 = \frac{2L}{c-u}\)

反射后光到达车尾需要

\(T_2 = \frac{2L}{c+u}\)

因此一共需要

\(T = T_1 + T_2 = \frac{2cL}{c^2 - v^2}\)

将前面的\(T = \frac{T'}{\sqrt{1 - (u/c)^2}}\) 代入，有

\(L = \sqrt{1 - (u/c)^2} * L'\)

即在站台上的人看来，长度缩短了。

时间膨胀和长度收缩证明

原文：https://www.cnblogs.com/qxred/p/time_dilation.html