题目描述：

在 N * N 的网格中，我们放置了一些与 x，y，z 三轴对齐的 1 * 1 * 1 立方体。

每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。

现在，我们查看这些立方体在 xy、yz 和 zx 平面上的投影。

投影就像影子，将三维形体映射到一个二维平面上。

在这里，从顶部、前面和侧面看立方体时，我们会看到“影子”。

返回所有三个投影的总面积。

示例 1：

输入：[[2]]
输出：5

示例 2：

输入：[[1,2],[3,4]]
输出：17
解释：
    这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

示例 3：

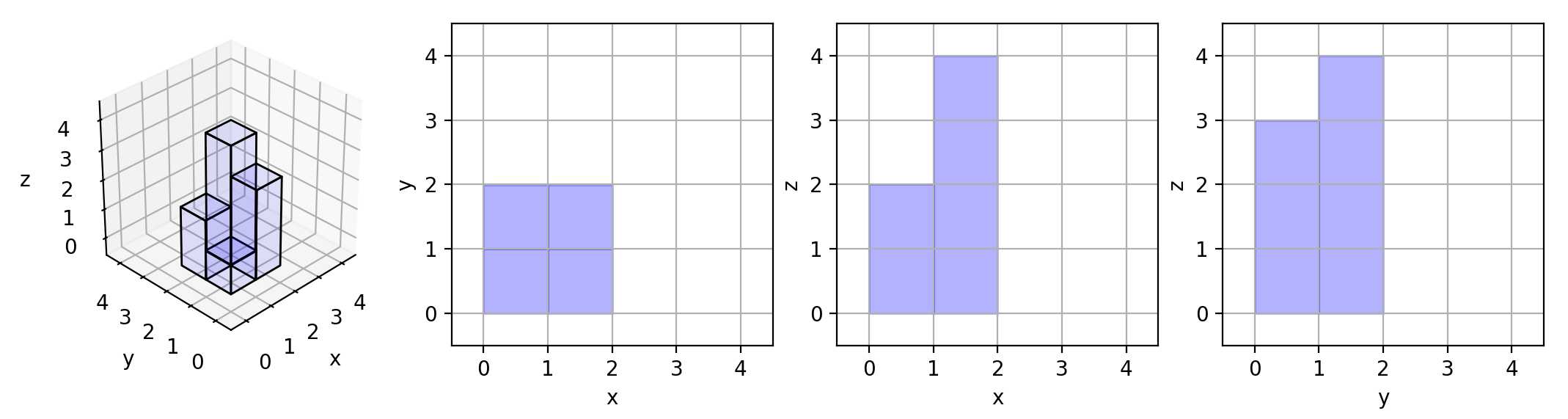
输入：[[1,0],[0,2]]
输出：8

示例 4：

输入：[[1,1,1],[1,0,1],[1,1,1]]
输出：14

示例 5：

输入：[[2,2,2],[2,1,2],[2,2,2]]
输出：21

提示：

• 1 <= grid.length = grid[0].length <= 50
• 0 <= grid[i][j] <= 50

解法：

class Solution {
public:
    int projectionArea(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<int> row(m, 0);
        vector<int> col(n, 0);
        int val = 0;
        for(int i = 0; i < m; i ++){
            for(int j = 0; j < n; j++){
                row[i] = max(row[i], grid[i][j]);
                col[j] = max(col[j], grid[i][j]);
                if(grid[i][j] != 0){
                    val++;
                }
            }
        }
        int res = val;
        for(int v : row){
            res += v;
        }
        for(int v : col){
            res += v;
        }
        return res;
    }
};

leetcode 883. 三维形体投影面积(Projection Area of 3D Shapes)

原文：https://www.cnblogs.com/zhanzq/p/10668620.html