文艺平衡树 Splay 学习笔记

好久之前就说要学Splay了，结果苟到现在才学习。

可能是最近良心发现自己实在太弱了，听数学又听不懂只好多学点不要脑子的数据结构。

感觉Splay比Treap良心多了——代码真的好写。

对于Splay显然可以维护Treap的所有操作，并且本质是BST。

先看看Splay是怎么维护普通平衡树操作的吧。

首先先定义一些基础的变量（若不作特殊说明这些变量的意义不变）

int t[N][2] // t[x][0]表示节点x的左子树,t[x][1]表示节点x的右子树

int cnt[N] // cnt[x]表示节点x存储多少个重复的数

int val[N] // val[x]表示节点x存储数的大小

int par[N] // par[x]表示节点x的直接父亲，特别的，根节点的直接父亲为0

int size[N] // size[x]表示在BST中x子树中存储数的个数

# define ls(x) (t[x][0])

# define rs(x) (t[x][1]) //方便书写

Check(x) 函数 :

询问节点x是其父亲的左儿子(return 0)还是右孩子(return 1)

int check (int x)  { 
    return rs(par[x])==x;
}

由上述代码可知，根节点的check(root)值为0，即根节点是0节点的左儿子(Nothing Special）

Up(x)函数：

对于节点x维护其size值为两个孩子的size值+自身cnt值。

void up(int x){
    size[x]=size[ls(x)]+size[rs(x)]+cnt[x];
}

Rotate(x)函数：

对于节点x旋转到其父亲节点，且不改变树BST性质。（使得树形态较为随机）

这里需要解释一下Rotate的解释和记忆方法（和Treap中Rotate类似）

对于一棵有根树（且父亲指向儿子的边有向），我们现在以把左儿子旋到父节点为例。

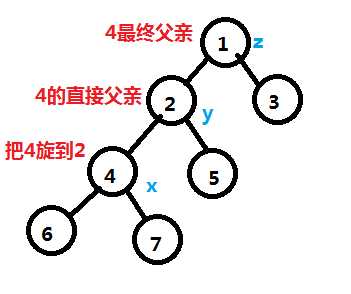
第1步，考虑4的右子树已经有元素了，考虑把右子树连接到父节点左儿子处。不改变BST性质。

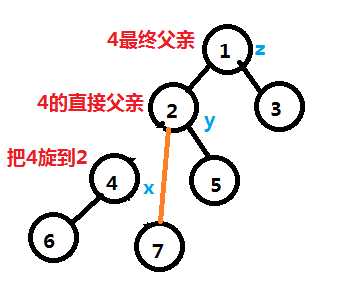
在此基础上考虑第二步，就是吧2（4的直接父亲接到4的右边）不改变BST性质。

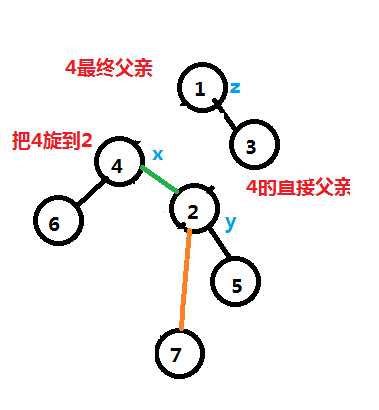
这个时候我们会发现，只进行第三部就可以完成一次rotate操作。

即连一条1指向4的边即可。

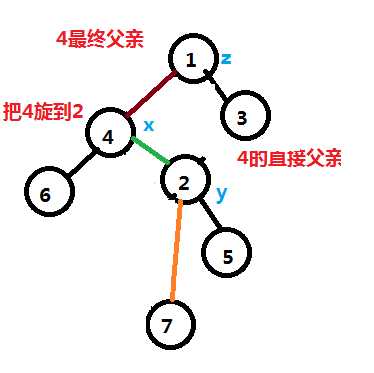
对于左边节点转到父亲节点，一般称之为右旋

对于右旋函数的代码，不难得到。

void rotate(int x){
  int y=par[x];
  t[y][0]=t[x][1]; par[t[x][1]]=y;
  t[x][1]=y; t[par[y]][check(y)]=x;
  par[x]=par[y]; par[y]=x;
  up(y); up(x);
}

右旋

那左旋呢？？？

所有0和1的地方去个反不就好了！！！(至少我是那么记的)

对于 真正的旋转代码：

void rotate(int x){
      int y=par[x],k=check(x);
      t[y][k]=t[x][k^1]; par[t[x][k^1]]=y;
      t[x][k^1]=y; t[par[y]][check(y)]=x;
      par[x]=par[y]; par[y]=x;
      up(y); up(x);
}

Splay(x,goal) 操作

把节点x通过若干次rotate操作使其到达目标节点goal或者为根，而goal却成为节点x的儿子。

我们可以分三种情况讨论：

1. goal 是 x的直接父亲（边界），那么直接将x旋到父亲位置即可

2. x和x的直接父亲y和x的爷爷z在同一条直线上(不会打结吗？我们需要给定一种顺序)

那么先旋转父亲y，再旋转x，这个时候想就被旋转到y和z节点上方了。

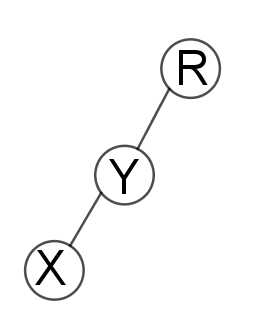
3. x和x的直接父亲y和x的爷爷z在不在同一条直线上（直接把x转两次不就行了么）

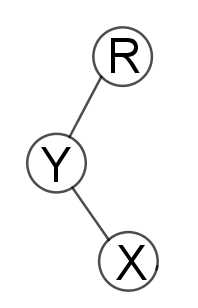
我们可以参考下图，模拟一条链上的Splay操作。

 简单的代码实现如下（自然语言是多么的无力....）

void splay(int x,int goal=0) {
    while (par[x]!=goal) {
        int y=par[x],z=par[y];
        if (z!=goal) {
            if (check(x)==check(y)) rotate(y);
            else rotate(x);
        }
        rotate(x);
    }
    if (!goal) root=x;
}

文艺平衡树 Splay 学习笔记

原文：https://www.cnblogs.com/ljc20020730/p/10597659.html