| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 41771 | Accepted: 16955 |
Description
Input
Output
Sample Input
3 3 1 2 2 1 2 3
Sample Output
1
Hint
Source
再Tarjan算法中,有如下定义。
DFN[ i ] : 在DFS中该节点被搜索的次序(时间戳)
LOW[ i ] : 为i或i的子树能够追溯到的最早的栈中节点的次序号
当DFN[ i ]==LOW[ i ]时,为i或i的子树可以构成一个强连通分量。
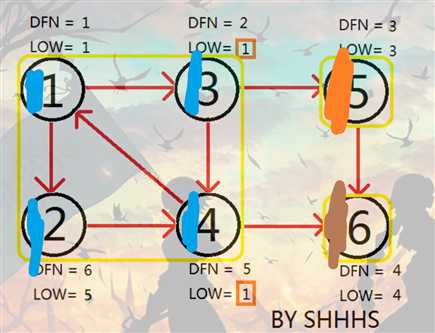
借这个图说明一下染色
为了打字 以下缩写DFN=LOW为条件
首先DFS 栈里面有1 3 5 6
到第六个节点 已经到达DFS最深处 满足条件 染成棕色 栈里面有1 3 5
返回到5 满足条件 染成橙色 栈里面有1 3
到3
再到4 4可以到1 但是不满足!dfn[v] , 它满足!color[v], low[id] = min(low[id], dfn[v]); low[4] = 1, 不满足条件 栈里面有 1 3 4
回到3 low[id] = min(low[id], low[v]); low[3] = 1, 不满足条件 栈里面有 1 3 4
到1
再到2 2可以到4 但是不满足!dfn[v] , 它满足!color[v], low[id] = min(low[id], dfn[v]); low[2] = 5, 不满足条件 栈里面有 1 3 4 2
再回到1 满足条件 把栈里面的都拿出来染成蓝色 完毕
注意要反向建图(是这样子叫么?)
#include <stdio.h>
#include <iostream>
#include <vector>
#include <algorithm>
int N, M;
using namespace std;
const int si = 10010;
vector<int> G[si];
int dfn[si], low[si], color[si], size[si], stk[si];
bool flag[si];
int timelag, colorcnt, stksize;
void tarjan(int id) {
dfn[id] = low[id] = ++timelag;
stk[stksize++] = id;
for (int i = 0; i < G[id].size(); i++) {
int v = G[id][i];
if (!dfn[v]) {//dfn也是vis的标志 是否来过
tarjan(v);
low[id] = min(low[id], low[v]);
}
else if (!color[v]) {
low[id] = min(low[id], dfn[v]);
}
}
if (dfn[id] == low[id]) {//染色
int cnt = 0;
colorcnt++;
while (stksize) {
stksize--;
int x = stk[stksize];
color[x] = colorcnt;
cnt++;
if (x == id) break;
}
size[colorcnt] = cnt;
}
}
int main() {
cin >> N >> M;
while (M--) {
int a, b;
scanf("%d %d", &a, &b);
G[b].push_back(a);//反向建图
}
for (int i = 1; i <= N; i++) {
if (!dfn[i]) tarjan(i);//求强连通分量 dfn也是vis的标志
}
for (int i = 1; i <= N; i++) {
for (int j = 0; j < G[i].size(); j++) {
int x = G[i][j];//i到x的边 但是他们不是同一个颜色的 上图的3和5是这种关系
if (color[i] != color[x]) flag[color[x]] = 1;
//x崇拜i 则x所处的强连通分量都崇拜i 所有与x颜色相同的都崇拜i
//但是i不崇拜x 否则i和x是同一个强连通分量同一种颜色了 所以扩大到整个x的颜色
}
}
int num = 0, ans = 0;
for (int i = 1; i <= colorcnt; i++) {
if (flag[i]) continue;
num++;
ans = size[i];
}
if (num != 1) ans = 0;//只会有一个被其它所有牛崇拜的强连通分量
cout << ans << endl;
return 0;
}
原文:https://www.cnblogs.com/smatrchen/p/10596563.html