Input
Output
Sample Input
1 5 1 4 2 6 8 10 3 4 7 10
Sample Output
4
题目大意:给你一堵墙,长为10000000 ,再给你若干份海报,海报的高度与墙的高度一致,再给出贴海报的位置,先贴的海报可以被覆盖。问贴完后你能看到多少张海报(即没有完全被覆盖的海报有多少张)
海报最多10000张,海报不会落在瓷砖中间(看上图容易理解)
解题思路:线段树+离散化+懒惰数组(线段树区间更新问题)
我们把贴海报看成在墙上涂颜色,颜色用数字表示,比如贴第一张海报,col就为1,贴第二张海报,col就为2
把线段树的节点表示出来:l,r表示该点的区间,col是该区间的颜色,val为1代表该区间只有一种颜色,val为0代表该区间没有被涂色或有多种颜色
struct node{
int l,r,col,val;
} tree[MAXN*8];
线段树的样子(以区间1-10为例子)
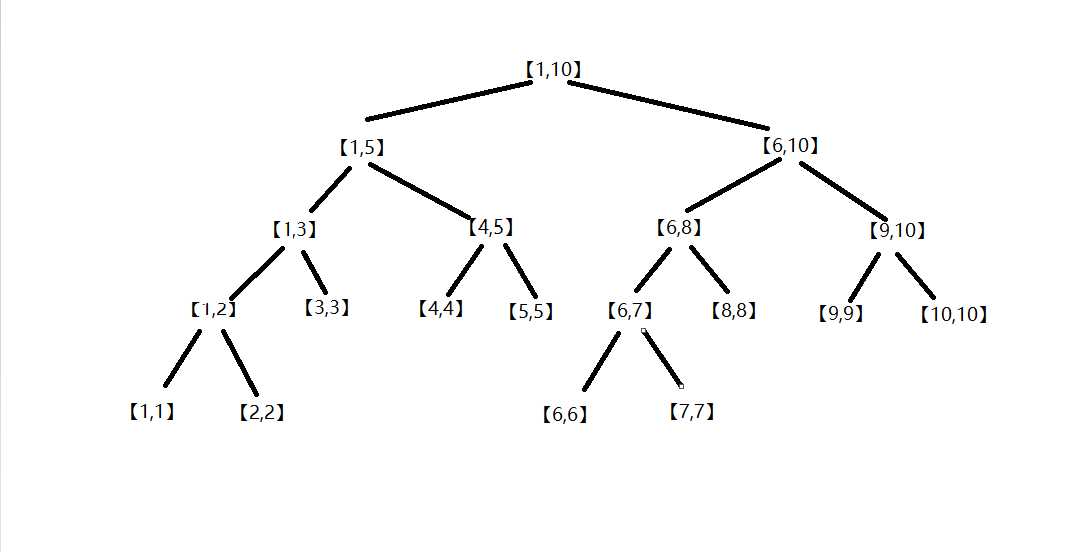
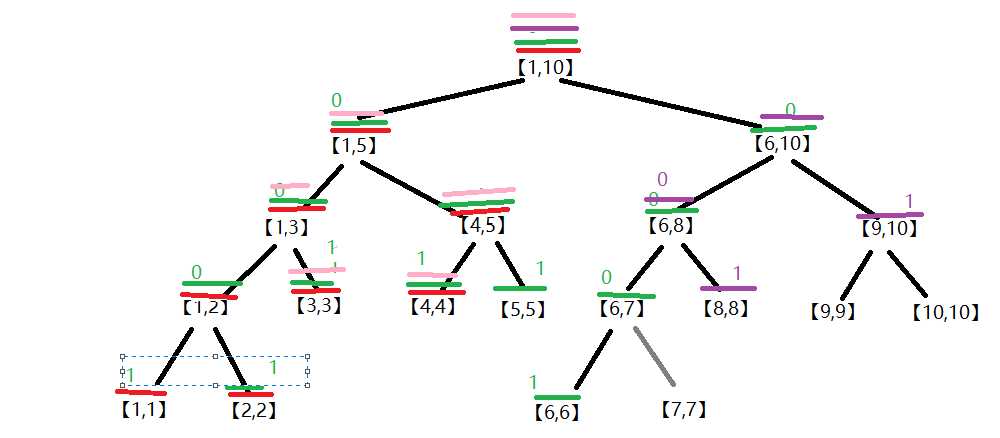
我们用这棵树来演示一遍解样例的过程
首先是建树,每个节点都是无色的(col为0),每个节点的val都是0;
然后是更新,一张一张海报往上贴
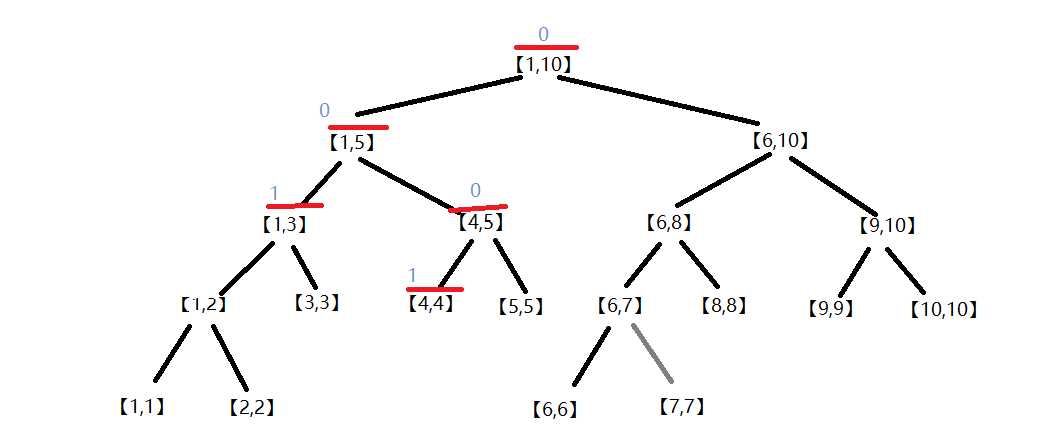
贴第一张,头顶红色的节点是扫描过的节点,其中【1,3】【4,4】的val改为1,因为这些区域都只有一种颜色而且全覆盖了
(节点上的数字是val的值)
第一张【1,4】
贴第二张,头顶绿色的就是第二遍更新扫描过的节点,注意看蓝色圈圈的部分,对比一下上图,发现【1,2】【3,3】【1,1】【2,2】都画上了红线。
一开始【1,3】涂了颜色1,说明【1,1】【2,2】【3,3】都是涂了颜色1,但是上图中这3个区间并没有被访问,这就是因为懒嘛。。。。
等到再次访问【1,3】这个点,并且要继续往下走的时候,才把【1,3】下面的两个节点涂上色,再进行处理,有种不到ddl死活不肯干活的感觉
不用懒惰标记:贴一张【1,9】的海报,就要把除了【10,10】之外的节点都访问一遍,共18次
用了懒惰标记:贴一张【1,9】的海报,访问【1,10】【1,5】【6,10】【6,8】【9,10】【9,9】共6次
这就是懒惰标记的作用,它可以减少很多运算并保证答案的正确性
第二张【2,6】
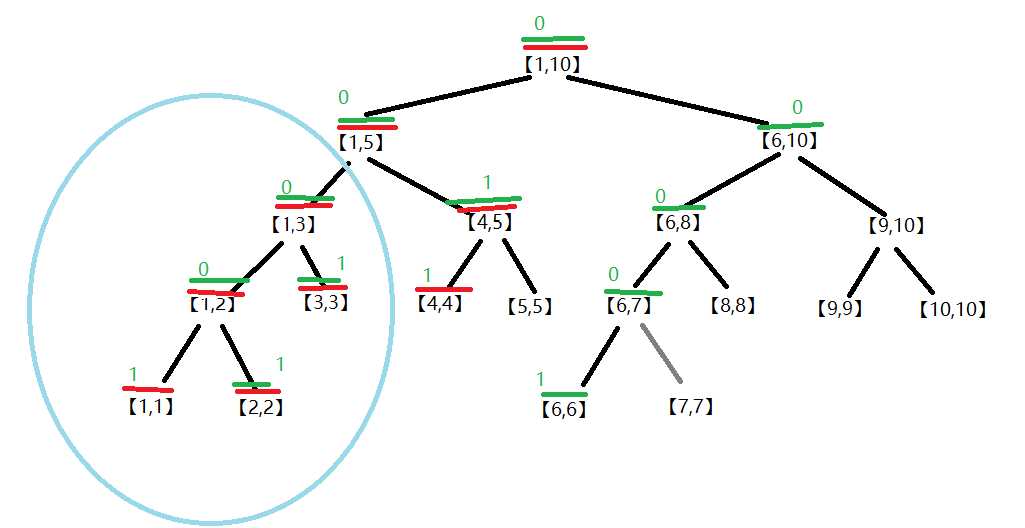
贴第三张【8,10】
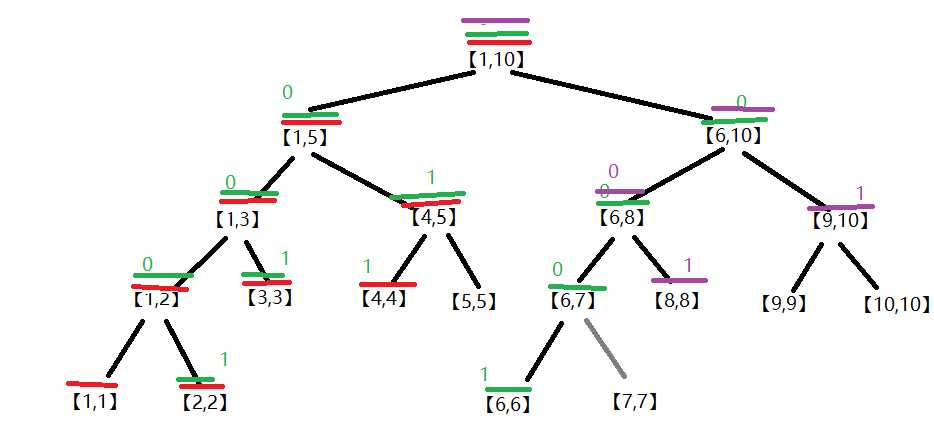
第四张【3,4】
第五张【7,10】
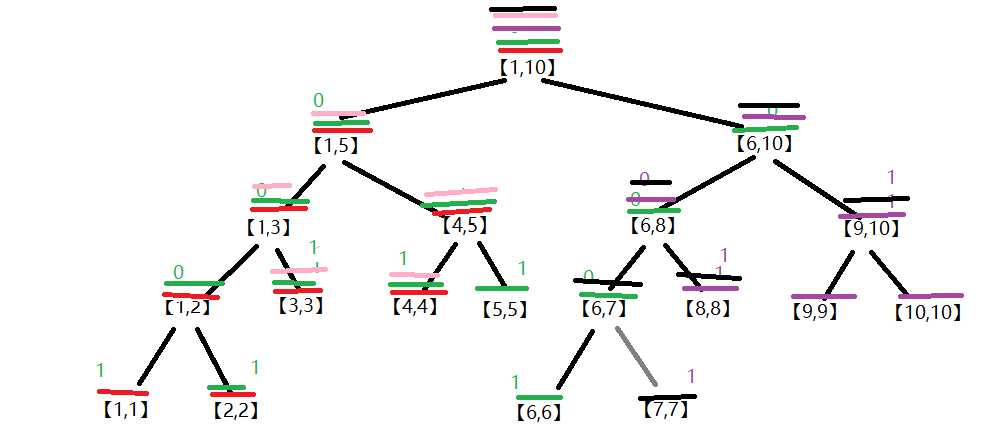
标记好了后开始查找query,找val=1的,每找到一个val等于1的就判断该颜色有没有出现过,没有则num++,有则忽略,返回上一层;
这里搜索下来就是【1,1】1色,【2,2】2色,【3,3】3色,【4,4】3色,【5,5】2色,【6,6】2色,【7,7】5色,【8,8】5色,【9,10】5色
一共4中颜色,即有4张可见海报
离散化
这个只是样例的解法,如果放到整个问题中,第一个节点的区间范围为【1,10000000】,显然直接开数组存会TLE或者MLE
这个时候我们就要对数据进行离散化
个人对离散化的理解,就相当于映射,下面用样例来做解释
一开始,我们有1,4,2,6,8,10,3,4,7,10十个点
把他们按从小到打的顺序排列,变成1,2,3,4,4,6,7,8,10,10
然后从1开始,给每个不同的数字进行编号

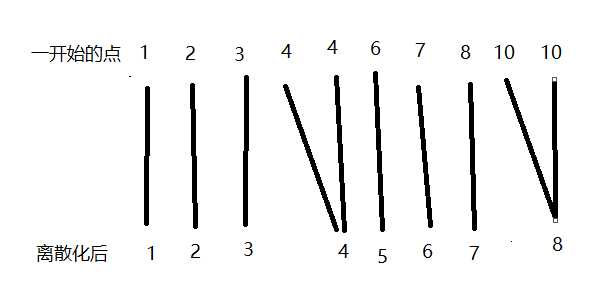
可以看出,用离散化后的点完全可以表示原来的点(就是映射啦)
而原来的点区间为【1,10】
离散化后的点区间为【1,8】
这里看好像不明显,但如果一开始的点中8换成了10000000
那么原来的点区间为【1,10000000】
离散化后的点区间还是【1,8】
区别就体现出来了
题目中海报最多10000张,最多有20000个点
离散化后区间是【1,20000】
和一开始的【1,10000000 】相比,显然........
用离散化后的数来建树,按照上面的思路就可以解题了
代码:
#include <iostream> #include <algorithm> #include <cmath> #include <string.h> #include <stdio.h> using namespace std; #define MAXN 10010 int N; struct node{ int l,r,col,val;//线段树的节点,内容包括区间l和r的值,颜色col(即哪张海报),val=1表示【l,r】为单色,val表示【l,r】不是单色 }tree[MAXN*8]; bool vis[MAXN];//判断该颜色是否出现过,查询时使用 struct point{ int a,n,f;//记录离散化前的点,a表示 点的值,n表示颜色(即哪张海报),f=0表示该点是区间左端点,f=1表示该点是区间右端点 }p[MAXN*2]; struct san{ int l,r,col;//记录离散化后的线段,l,r是左右端点,col是颜色,下标表示哪张海报 }in[MAXN]; bool cmp(point a,point b) { return a.a <b.a ; } void build(int l,int r,int rt)//l是左端点,r是右端点,rt是当前节点 { tree[rt].l=l; tree[rt].r=r; tree[rt].val=0; tree[rt].col=0; if(l==r) return ; int mid=(l+r)>>1; build(l,mid,rt<<1); build(mid+1,r,rt<<1|1); } void updata(int l,int r,int col,int rt)//l是更新的左端点,r是更新的右端点,col是更新的颜色,rt是当前节点 { if(tree[rt].val&&tree[rt].col==col) return ; //如果当前线段是单色而且 该线段的颜色和要更新的颜色一致,则不用改了,返回 if(tree[rt].l==l&&tree[rt].r==r){//找到要更新的线段 tree[rt].col=col; tree[rt].val=1; return; } if(tree[rt].val ){//懒惰标记,把懒惰标记打在2个孩子身上,自己的懒惰标记取消 tree[rt<<1].val=tree[rt<<1|1].val=tree[rt].val; tree[rt<<1].col=tree[rt<<1|1].col=tree[rt].col; tree[rt].val=0; } int mid=(tree[rt].l+tree[rt].r)>>1; if(l>mid) updata(l,r,col,rt<<1|1);//要更新的线段在右孩子上 else if(r<=mid) updata(l,r,col,rt<<1);//要更新的线段在左孩子上 else {//要更新的线段在左右孩子上 updata(l,mid,col,rt<<1); updata(mid+1,r,col,rt<<1|1); } } int query(int l,int r,int rt) { int col=tree[rt].col; if(tree[rt].val){//线段单色 if(!vis[col]) {//该颜色没有出现过 vis[col]=1; return 1;//该颜色出现了,查找多了一种颜色 } else return 0;//这种颜色出现过了 } int mid=(tree[rt].l+tree[rt].r)>>1; return query(l,mid,rt<<1)+query(mid+1,r,rt<<1|1); //找左右孩子 } int main() { int M; scanf("%d",&M); while(M--) { scanf("%d",&N); for(int i=1;i<=N;++i){ int a,b; scanf("%d %d",&a,&b); p[2*i-1].a=a; p[2*i-1].n=i; p[2*i-1].f=0; p[2*i].a=b; p[2*i].n=i; p[2*i].f=1; //存海报,一共有N条线段,2N个点 } //离散化开始 sort(p+1,p+1+2*N,cmp); p[0].a=p[1].a;//为循环设一个特殊条件 int num=1,n,f;//num表示有多少个离散化后的点 for(int i=1;i<=2*N;++i){ n=p[i].n; f=p[i].f; if(p[i].a!=p[i-1].a) num++; if(!f) {//该点是起点 in[n].l=num; in[n].col=n; } else {//该点是终点 in[n].r=num; in[n].col=n; } } //离散化结束 build(1,num,1);//建树,区间为【1,num】 for(int i=1;i<=N;++i)//区间更新,相当于贴海报的过程 updata(in[i].l,in[i].r,in[i].col,1); memset(vis,0,sizeof(vis)); printf("%d\n",query(1,num,1)); } }
原文:https://www.cnblogs.com/Remilia-Scarlet/p/10575744.html