$CROI$ $R1$
今天参加了一场比赛,什么比赛呢?CROI。
CROI是什么呢? $Challestend$ $Rehtorbegnaro$ $OI$。总的来说就是我们机房的一些神仙出的题啦。
T1:Challestend and Hyperrectangle
一道特别神仙的题目。
题意概述一下:给出一个高维立方体的 $n$ 个边长,将它的表面刷上漆,再将它切成单位小块,求恰好有 $i$ 面被着色的小立方体个数,对998244353取模.$i \in [0,2n]$,$4<=n<=30000,1<=a_i<=2^{64}$.
不会做呀...本来是有一点想法的,就是从一二三维的简单情况开始,进行类比,推出来一个比较科学的式子(它甚至可以过一个比较大的样例),但是对于 $a<=2$ 的情况就会崩溃,而且小一点的数据里每个都有这种情况,所以最后也没有分了。还是讲一下思路:
一维:两个顶点,$a-2$个无色立方体;
二维:四个顶点,$2\times(a-2+b-2)$个棱上的点,$(a-2)(b-2)$个无色立方体;
三维:八个顶点,$4\times(a-2+b-2+c-2)$个棱上的点,$2\times((a-2)(b-2)+(a-2)(c-2)+(b-2)(c-2))$个面上的点,$(a-2)(b-2)(c-2)$个无色的;
一维二维的可能比较难想,在这里放个图:

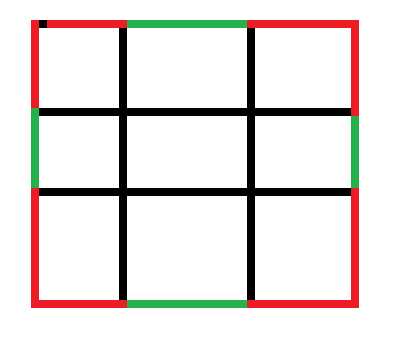
这题比较玄学的一点就是怎么分辨 $n$ 维立方体的“面”,因为按照一般的思路来说,只有三维立方体才有“面”。不过通过看样例,可以发现这道题里的“面”指的就是 $n-1$ 维的空间啦。
T2:Challestend and Anarchy Heap
这道题还是比较简单的(虽然我没做出来)。


题意概述:将斐波那契数顺次插入一个二叉堆,比较函数是随机的,问每次插入后堆顶的期望值的和,对998244353取模。$T<=400,1<=n<2^{64}$
虽然比较函数坏掉了,但是树的形态还是固定的。可以发现每次插入新数后,堆顶要么是新数,要么不变。考虑是新数的概率:新数运气超好,一路随机上来到了根,也就是$x=\text{当前点离根节点的距离},\frac{1}{2^{x}}$,其它情况下都不变。递推可以做到 $O(N)$,但是显然跑不过,所以可以矩乘,但是因为深度不固定,还得分段矩乘,有一点难写。
原文:https://www.cnblogs.com/shzr/p/10566947.html