在前面所介绍的线性回归, 岭回归和Lasso回归这三种回归模型中, 其输出变量均为连续型, 比如常见的线性回归模型为:
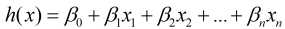
其写成矩阵形式为:
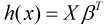
现在这里的输出为连续型变量, 但是实际中会有"输出为离散型变量"这样的需求, 比如给定特征预测是否离职(1表示离职, 0表示不离职). 显然这时不能直接使用线性回归模型, 而逻辑回归就派上用场了.
引用百度百科定义
逻辑(logistic)回归, 又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。
也就是说逻辑回归是从线性回归模型推广而来的, 我们从假设函数开始说起.
1. 假设函数
现假设因变量取值0和1, 在自变量X的条件下因变量y=1的概率为p, 记作p=P(y=1|X), 那么y=0的概率就为1-p, 把因变量取1和取0的概率比值p/(1-p)称为优势比, 对优势比取自然对数, 则可以得到Sigmoid函数:
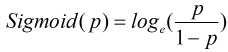
令Sigmoid(p)=z, 则有:
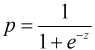
而Logistic回归模型则是建立在Sigmoid函数和自变量的线性回归模型之上(这可能就是为什么带有"回归"二字的原因吧), 那么Logistic回归模型可以表示为:
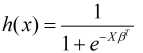
上式也常常被称为逻辑回归模型的假设函数, 其函数图像为:
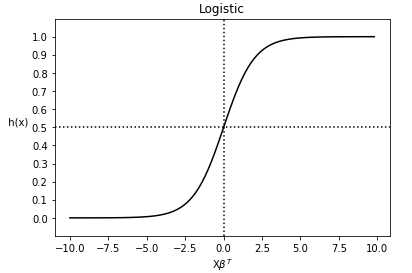
通过图像可以看出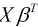
的取值范围为
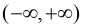, h(x)的取值范围为[0, 1], 对于二分类问题来说, h(x)>=0.5则y=1, h(x)<0.5则y=0, 而且通过图像得知: 当
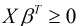时, h(x)>=0.5, 因此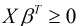时y=1, 否则y=0.
模型的假设函数知道了, 接下来看看损失函数.
2. 损失函数
既然逻辑回归是建立在线性回归模型之上, 那么我们先来回顾线性回归的损失函数:
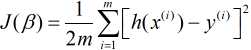
如果将我们逻辑回归的假设函数代入上式损失函数, 绘制出来的图像则是非凸函数, 其很容易产生局部最优解, 而非全局最优解, 为了找到使得全局最优解, 我们需要构造一个凸函数.
由于对数函数能够简化计算过程, 因此这里也是通过对数函数来构建, 先来回归下对数函数的图像(原图来自百度百科):
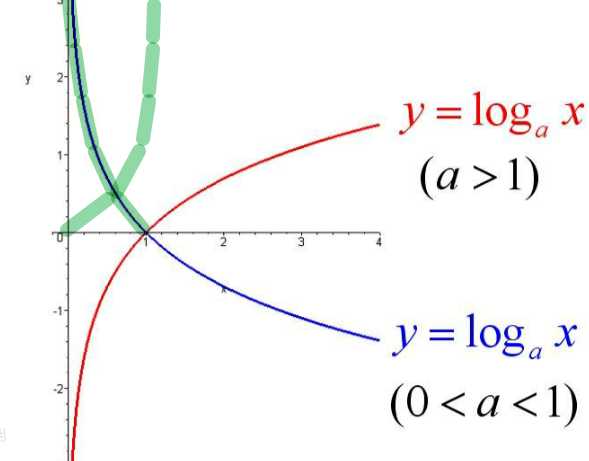
通过上图可以发现绿线部分与我们要构造的凸函数较接近. 当a=e时, 绿线部分可以分别表示为: -loge(x)和-loge(1-x). 现将x替换为h(x)并同时加入输出变量y (取值为1或0), 则有:
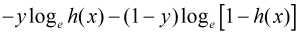
当上式中的y=1时, 其结果为-logeh(x); 当y=0时, 其结果-loge[1-h(x)].
最后, 将上式代入我们的损失函数中, 则有:
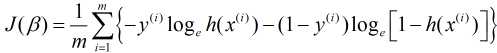
当然, 也可以用统计学中的极大似然法构造出上式损失函数. 损失函数有了, 下一步则是求解损失函数最小的算法了.
3. 算法
常用的求解算法有梯度下降法, 坐标轴下降法, 拟牛顿法. 下面只介绍梯度下降法(其他方法还未涉及)
你也许会有疑问, 既然是线性回归模型推广而来, 那么为什么没有最小二乘法呢? 最小二乘法是用来求解最小误差平方和的算法, 而误差的平方和正是我们上面提到的线性回归的损失函数, 通过其构造出来的逻辑回归的损失函数是非凸的不容易找到全局最优解, 故不选用最小二乘法, 而通过极大似然法则可以构造出凸函数, 进而可以使用梯度下降法进行求解.
对于梯度下降法的理解在这节, 这里直接给出其表示:
具体的求解过程:
因此, 我们的梯度下降法可以写成(其中, x0=1):
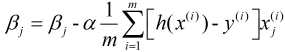
上式也被称为批量梯度下降法, 另外两种: 随机梯度下降法和小批量梯度下降法分别表示为:
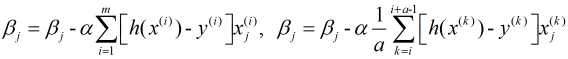
1. 优点
1) 模型简单, 训练速度快, 且对于输出变量有很好的概率解释
2) 可以适用连续型和离散型自变量.
3) 可以根据实际需求设定具体的阀值
2. 缺点
1) 只能处理二分类问题.
2) 适用较大样本量, 这是由于极大似然估计在较小样本量中表现较差.
3) 由于其是基于线性回归模型之上, 因此其同样会出现多重共线性问题.
4) 很难处理数据不均衡问题
3. 优化
1) 可以在二分类上进行推广, 将其推广到多分类回归模型
2) 对于多重共线性问题, 也可以通过删除自变量, 进行数据变换, 正则化, 逐步回归, 主成分分析等方法改善, 对于正则化逻辑回归同样有两种: L1和L2, 其分别表示为:
L1正则化
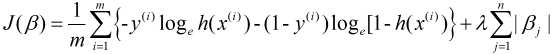
L2正则化
原文：https://www.cnblogs.com/star-zhao/p/10543640.html