快速幂

快速幂就是快速算底数的n次幂。其时间复杂度为 O(logN)。快速幂运算，可以看做是按位进行的一种取幂运算（二进制的伟大之处）。

　　Eg：以2 的4次方为例：

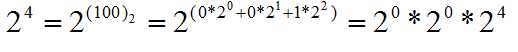
从上面的式子中，我们可以看出来，当指数的某一位是0的时候，我们可以忽略掉这一位，当指数不为0的时候乘上我们累计的底数(乘的是2^2);

Code：

1 int qPow(int x, int n){
2     int ans = 1, base = x;
3     while(n > 0){
4         if(n & 1) ans *= base; // 指数该位不为0
5         base *= base;  // 累乘
6         n >>= 1;  // 右移一位，磨平最右边的那位数字。
7     }
8     return ans;
9 } 

在有的时候我们需要对产生的解进行取余，如过底数和指数都特别大呐？取余岂不是特别费事，这时候我们就需要运用快速幂取余公式了

（a * b）% mod = ( ( a % mod ) * ( b % mod ) ) % mod ;

练习：HDU_1097

快速幂

原文：https://www.cnblogs.com/cgx249/p/10500435.html