猫树是一个有趣的数据结构,之前一直觉得这玩意儿应该很玄学,但学了之后发现还是挺朴素也挺好打的数据结构
要说两者之间的区别,大概就是询问(和修改)的复杂度了
首先线段树的询问复杂度肯定是 \(O(\log n)\) 的,这点没什么毛病吧?
然后猫树的询问复杂度呢?猫树的询问复杂度是 \(O(1)\)
这就是猫树的优势了,询问 O 1 ,少一个 log 的话,大概是几十倍的时间,但亲测大概速度也就比普通线段树快了一倍
究其原因的话还是普通线段树的 log 基本是跑不满的(所以说可能我数据造太烂了吧...)
但是不要小看这个“快一两倍”,这已经不是常数的问题了啊!(何况这只是我不大靠谱的测试)
就好像莫队的小优化能快个将近一倍之类的...
那么修改?
线段树当然还是 \(O(\log n)\)
但是猫树就要 \(O(n)\) 了,这个等到下面讲算法思路的时候就会提到了
所以说基本上猫树不用在待修改的区间询问题中(瞬间感觉没什么用了)
听你这么说,猫树不就是 ST 表么?
那么其实两者并不一样,因为他们能维护的信息范围不一样
线段树能维护的信息猫树基本都能维护,比如什么区间和、区间 gcd 、最大子段和 等 满足结合律且支持快速合并的信息
但是普通的 ST 表能够处理最大子段和么?(普通的 st 表当然不行,但用上猫树的思想就不一定了,博主没试过,有兴趣的读者可以考虑一下...)
说了这么多,该谈谈算法实现了吧?
我们假设当前查询的区间为 l , r
那么我们是不是可以考虑把这个区间分成两份,然后如果我们已经预处理除了这两个区间的信息,是不是就可以合并得到答案了呢?
那么现在的问题就是怎么预处理这两个区间的信息
其实关键就是要考虑可以使得任意一种区间都能被分成两份处理过的区间
那么我们先考虑用线段树中类似分治的思想,预处理区间信息
我们考虑把 1~n 整个区间分成两份 1~mid , mid+1~n
然后对于两分区间,我们先从 mid 和 mid+1 出发,\(O(n)\) 地像两边去遍历区间中的每个元素,同时维护要处理的信息
等两个区间都处理完之后,我们再向下递归,将两个区间继续分下去,即迭代以上步骤直到区间表示的只有一个数
那么这样的复杂度是 \(O(n\log n)\) 的,也就是预处理的复杂度并不比线段树差了
但是这里又有了一个问题: 我们之前说过的要满足每个区间都能被分成两份预处理过的区间
那么我们就要证明这样的预处理能满足以上条件了
proof:
我们看图说话

我们可以发现,当选择任意两个点后,这两个点之间的区间必然可以用他们在这颗线段树上的 \(LCA\) 的中间点必然可以将这个区间分成两段已处理过信息的区间
你可以随意尝试一下(当然我图画的有点...)
(为什么会这么神奇...)
证明一下,我们先将当前的两个点表示在根节点上
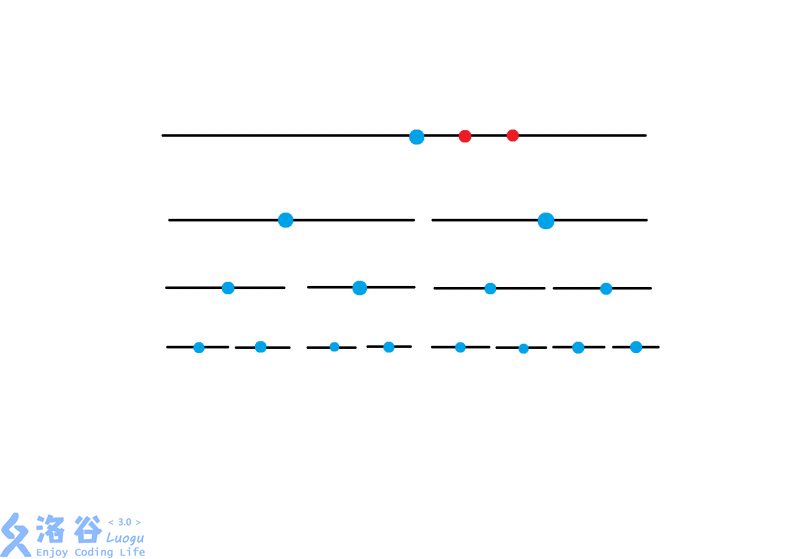
我们发现这两个点并不能被当前所在点的中间点分为两份,于是我们将他们下移进入右节点
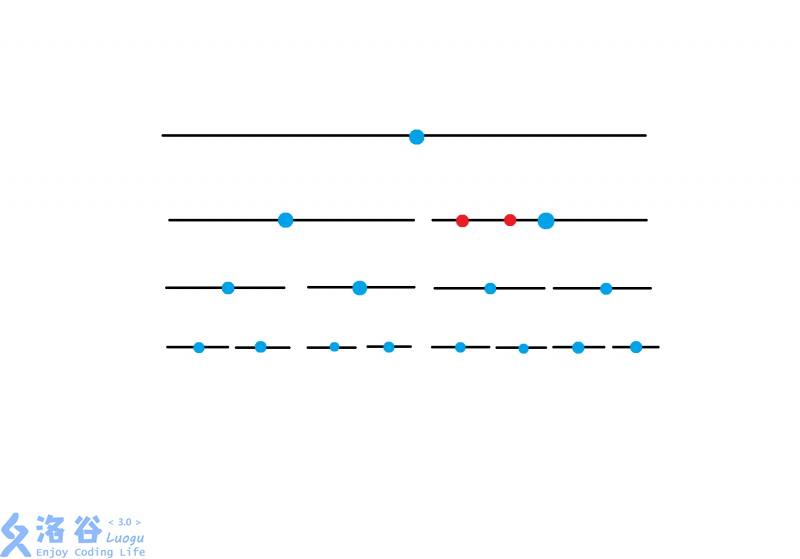
我们发现还是不能被中间点分成两份,继续下移
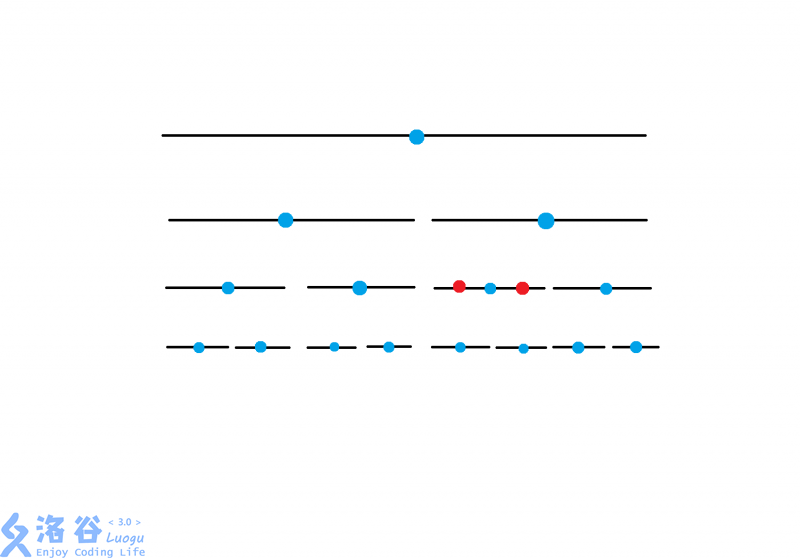
最后我们总能发现可以成功分割
但是呢,按照上面的找寻分割点的方法,我们发现好像复杂度还是 \(O(n)\)的?(难道复杂度是假的?)
别急,上面只是证明分割的可行性,并不是找寻分割点的方法
之前我们有提到分割点在 \(LCA\) 上,所以我们只需要处理出 \(LCA\) 的位置就好了,难道用树剖或是倍增?复杂度还是没变啊!顶多变成了 \(O(loglogn)\) 啊!
我们观察一下就可以发现(或者说根据线段树的性质来说),线段树中两个叶子结点的 \(LCA\) 其实就是他们位置编号的最长公共前缀(二进制下)
eg : \((10001)_2 (10110)_2\) 两个节点的 \(LCA\) 就是 \((10)_2\)
那么怎么快速求出两个数的最长公共前缀?
这里要用到非常妙的一个办法:
我们将两个数异或之后可以发现他们的公共前缀不见了,即最高位的位置后移了 \(\log LCA.len\) , 其中 \(LCA.len\) 表示 \(LCA\) 节点在二进制下的长度
那么我们就可以预处理一下 log 数组,然后在询问的时候就可以快速求出两个询问节点的 \(LCA\) 所在的 层 了
等等,层?不用求出编号的么?
这里解释一下,为了省空间,我们考虑将同一层处理出的信息放在一个数组里,毕竟他们互相之间没有相交
并且,这么做的话,查询的时候就只需要得到 \(LCA\) 所在层,然后将 l、 r 直接带入就可以合并求解了
以处理区间最大子段和为例:
//by Judge
#include<cstdio>
#include<iostream>
#define ll long long
using namespace std;
const int M=2e5+3;
#ifndef Judge
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
#endif
char buf[1<<21],*p1=buf,*p2=buf;
inline int read(){ int x=0,f=1; char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f;
} char sr[1<<21],z[20];int C=-1,Z;
inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;}
inline void print(int x,char chr='\n'){
if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x;
while(z[++Z]=x%10+48,x/=10);
while(sr[++C]=z[Z],--Z);sr[++C]=chr;
} int n,m,a[M],len,lg[M<<2],pos[M],p[21][M],s[21][M];
// p 数组为区间最大子段和, s 数组为包含端点的最大子段和
inline int Max(int a,int b){return a>b?a:b;}
#define ls k<<1
#define rs k<<1|1
#define mid (l+r>>1)
#define lson ls,l,mid
#define rson rs,mid+1,r
void build(int k,int l,int r,int d){
if(l==r) return pos[l]=k,void(); int prep,sm;
// 处理左半部分
p[d][mid]=s[d][mid]=prep=sm=a[mid],sm=Max(sm,0);
for(int i=mid-1;i>=l;--i)
prep+=a[i],sm+=a[i],s[d][i]=Max(s[d][i+1],prep),
p[d][i]=Max(p[d][i+1],sm),sm=Max(sm,0);
// 处理右半部分
p[d][mid+1]=s[d][mid+1]=prep=sm=a[mid+1],sm=Max(sm,0);
for(int i=mid+2;i<=r;++i)
prep+=a[i],sm+=a[i],s[d][i]=Max(s[d][i-1],prep),
p[d][i]=Max(p[d][i-1],sm),sm=Max(sm,0);
build(lson,d+1),build(rson,d+1); //向下递归
}
inline int query(int l,int r){ if(l==r) return a[l];
int d=lg[pos[l]]-lg[pos[l]^pos[r]]; //得到 lca 所在层
return Max(Max(p[d][l],p[d][r]),s[d][l]+s[d][r]);
}
int main(){ n=read(),len=2;
while(len<n) len<<=1;
for(int i=1;i<=n;++i) a[i]=read();
for(int i=2,l=len<<1;i<=l;++i)
lg[i]=lg[i>>1]+1;
build(1,1,len,1);
for(int m=read(),l,r;m;--m)
l=read(),r=read(),
print(query(l,r));
return Ot(),0;
}码量其实会少很多,可以看到最主要的码量就在 \(build\) 里面,但是 \(build\) 函数的思路还是很清晰的
就是上面的板子
其他的能拿来当纯模板的基本找不到(可见限制还是蛮大的,毕竟带修改的不行),不过一些要拿线段树来优化的题目(比如线段树优化 dp )还是可以用上的...吧?
参考资料:%%%zjp大佬
原文:https://www.cnblogs.com/Judge/p/10475728.html