数是一种抽象的数据类型(ADT)或是作这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合,它是由n(n>1)的有限个节点和节点之间的边组成的一个有层次关系的集合。
树的种类
如下图所示:
满二叉树:
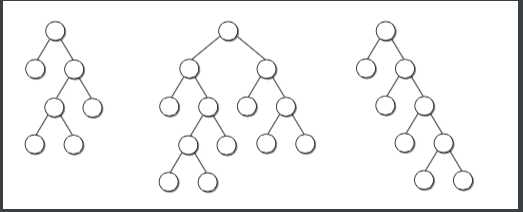
完美二叉树:
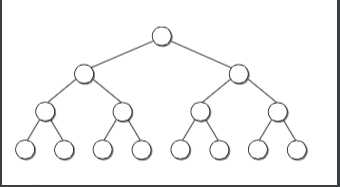
完全二叉树:
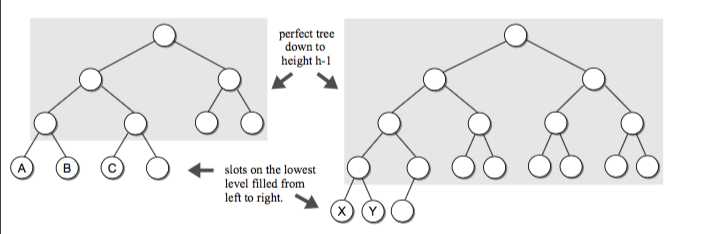
顺序存储:将数据结构存储在固定的数组中,所以在遍历速度上有一定的优势,同时所占用的空间比较大,是非主流二叉树。二叉树通常以链式方式存储:
如下图所示是简单的顺序存储:
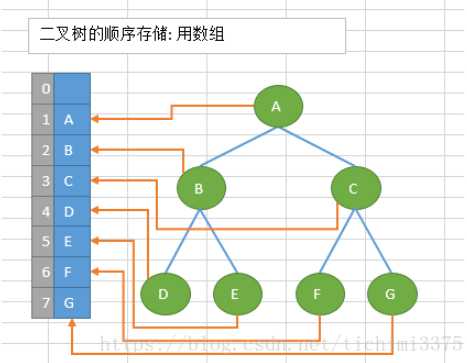
链式存储: 结构采用链表存储二叉树中的数据元素,用链表建立二叉树中节点之间关系,二叉树最常用的链式存储结构是二叉链,每个节点包含三个域,分别是数据元素域data,
左还在链域Child和右孩子链域Child,与单链表头结点和不带头节点的两种情况相似,二叉链存储结构的二叉树也有带头节点和不带头结点两种。
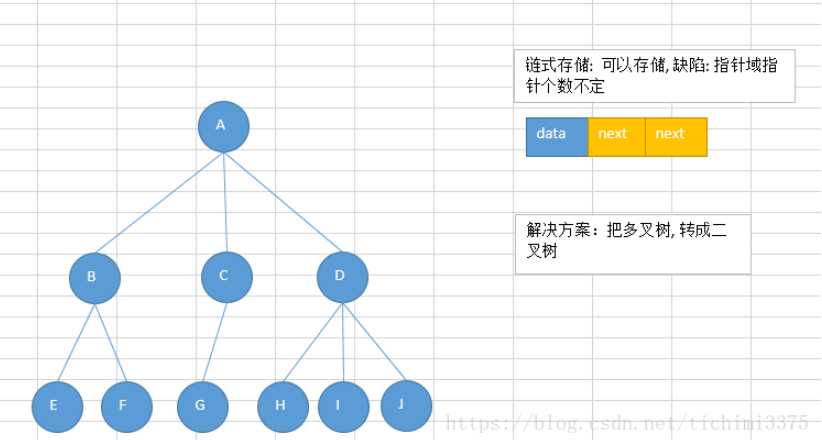
二叉树是由n(n>=0)个节点组成的集合,每个节点最多有两个子树的有序树,它或者是空集,或者是一个根和左右子树的两个不相交的二叉树组成。
二叉树的特点:
二叉树是有序树,即使是只有一个子树,也必须区分左右树。
二叉树的每个节点的的度,不能大于2.
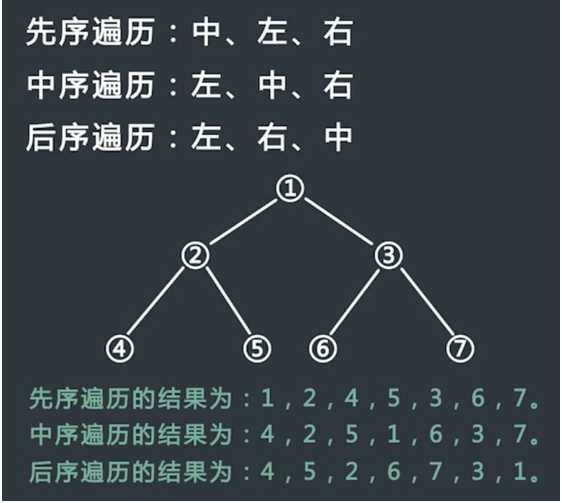
前序遍历:先访问根节点, 然后前序遍历左子树,再前序遍历右子树
中序遍历:中序遍历根节点的左子树,然后再访问根节点,最后遍历右子树
后序遍历:从左到右叶子节点的方式遍历访问左子树,最后访问根节点
层序遍历:从根节点从上往下逐层遍历,在同一层,按从左到右的顺序对节点逐个访问
# 节点定义 class Node(object): def __init__(self, value, left_child, right_child): self._value = value self._left_child = left_child self._right_child = right_child @property def value(self): return self._value @value.setter def value(self, value): self._value = self.value @property def left_child(self): return self._left_child @left_child.setter def left_child(self, value): self._left_child = value @property def right_child(self): return self._right_child @right_child.setter def right_child(self, value): self._right_child = value # 树的定义 class Tree(object): def __init__(self, value): self._root = Node(value, None, None) @property def root(self): return self._root
# 递归后续遍历 def pre_order(root): if not isinstance(root, Node): return [] pre_order_tmp = [] if root is not None: pre_order_tmp.append(root.value) pre_order_tmp += pre_order(root.left_child) pre_order_tmp += pre_order(root.right_child) return pre_order_tmp # 非递归后续遍历 def pre_order_not_recursion(root): if not isinstance(root, Node): return None stack = [root] result = [] while stack: node = stack.pop(-1) if node: if isinstance(node, Node): result.append(node.value) stack.append(node.right_child) stack.append(node.left_child) else: result.append(node) return result # 递归中序遍历 def middle_order(root): if not isinstance(root, Node): return [] middle_order_tmp = [] if root is not None: middle_order_tmp += middle_order(root.left_child) middle_order_tmp.append(root.value) middle_order_tmp += middle_order(root.right_child) return middle_order_tmp # 非递归中序遍历 def middle_order_not_recursion(root): if not isinstance(root, Node): return None stack = [root.right_child, root.value, root.left_child] result = [] while stack: node = stack.pop(-1) if node: if isinstance(node, Node): stack.append(node.left_child) stack.append(node.value) stack.append(node.right_child) else: result.append(node) return result # 递归后续遍历 def post_order(root): if not isinstance(root, Node): return [] post_order_tmp=[] if root is not None: post_order_tmp += pre_order(root.left_child) post_order_tmp += pre_order(root.right_child) post_order_tmp.append(root.value) return post_order_tmp # 非递归后续遍历 def post_order_recursion(root): if not isinstance(root, Node): return None stack = [root.value, root.right_child, root.left_child] result = [] while stack: node = stack.pop(-1) if node: if isinstance(node, Node): result.append(node.value) stack.append(node.right_child) stack.append(node.left_child) else: result.append(node) return result # 分层遍历 def layer_order(root): if not isinstance(root, Node): return [] queue = [root.value, root.left_child, root.right_child] result = [] while queue: tmp = queue.pop(0) if tmp: if isinstance(tmp, Node): queue.append(tmp.value) queue.append(tmp.left_child) queue.append(tmp.right_child) else: result.append(tmp) return result
# 递归方式计算节点个数 def node_count(root): if not isinstance(root, Node): return None else: if root: return node_count(root.left_child)+node_count(root.right_child)+1 else: return None # 借用分层遍历实现 def node_count_not_recursion(root): if not isinstance(root, Node): return None return len(layer_order(root)) # 计算二叉树深度 def tree_deep(root): if not isinstance(root, Node): return None if root: return 1+max(tree_deep(root.left_child), max(root.right_child)) else: return 0 # 非递归方式实现 def tree_deep_not_recursion(root): if not isinstance(root, Node): return None stack = [(root, 1)] result = 0 while stack: tmp_node, tmp_layer = stack.pop(0) if tmp_node: stack.append((tmp_node.left_child, tmp_layer+1)) stack.append((tmp_node.ritht_child, tmp_layer+1)) result = tmp_layer+1 return result # 计算第K层节点的个数 def kth_node_count(root, k): if not isinstance(root, Node): return None if not root or k <=0: return 0 if k == 1: return 1 return kth_node_count(root.left_child, k-1)+kth_node_count(root.right_child, k-1) # 计算二叉树叶子节点的个数 def leaf_account(root): if not isinstance(root, Node): return None if not root: return 0 if not root.left_child and not root.right_child: return 1 return leaf_account(root.left_child)+leaf_account(root.right_child) # 判断是否为二分查找树BST # 判断是否为二分查找树BST,递归方式 # 二分查找树的定义搞清楚,二分查找树的中序遍历结果为递增序列 def is_bst_tree(root): if not isinstance(root, Node): return [] def is_asc(order): for i in range(len(order)-1): if order[i] > order[i+1]: return False return True return is_asc(middle_order_not_recursion(root)) if __name__ == ‘__main__‘: tree = Tree(1) tree1 = Tree(1) node7 = Node(5, None,None) node6 = Node(4, None,None) node5 = Node(3, None,None) node4 = Node(2, None,None) node3 = Node(1, None,None) node2 = Node(3, node5, node6) node1 = Node(4, node3, node4) tree.root.left_child = node1 tree.root.right_child = node2 tree1.root.left_child = node2 tree1.root.right_child = node2 print (post_order_recursion(tree.root)) print(is_bst_tree(tree.root)) print(is_bst_tree(tree1.root))
原文:https://www.cnblogs.com/tashanzhishi/p/10448425.html