并查集,顾名思义,就是将集合合并及其查询,为了便于讲解,我先将题目及完整代码贴至下方,不理解的可以先看看熟悉一下,下方会有详细讲解。
详情请见洛谷p3367
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。
输入格式:
第一行包含两个整数N、M,表示共有N个元素和M个操作。
接下来M行,每行包含三个整数Zi、Xi、Yi
当Zi=1时,将Xi与Yi所在的集合合并
当Zi=2时,输出Xi与Yi是否在同一集合内,是的话输出Y;否则话输出N
输出格式:
如上,对于每一个Zi=2的操作,都有一行输出,每行包含一个大写字母,为Y或者N。
(此处代码未经过优化,如何优化详见下文)(大雾)
#include<bits/stdc++.h>
using namespace std;
int group[100001],N,M;
int get_father(int x)
{
return (group[x]==x)?x:get_father(group[x]);
}
int main()
{
int selected;
cin>>N>>M;
for(int i=1;i<N;i++)
{
group[i]=i;
}
for(int i=1;i<=M;i++)
{
cin>>selected;
if(selected==1)
{
int X,Y;
cin>>X>>Y;
group[get_father(X)]=get_father(Y);
}
if(selected==2)
{
int X,Y;
cin>>X>>Y;
if(get_father(group[X])==get_father(group[Y]))
{
cout<<"Y"<<endl;
}
else
{
cout<<"N"<<endl;
}
}
}
return 0;
}
举个栗子:假设有十个点并且X-->Y代表X的父亲是Y。
先放个友好的图(画工很好不是吗)
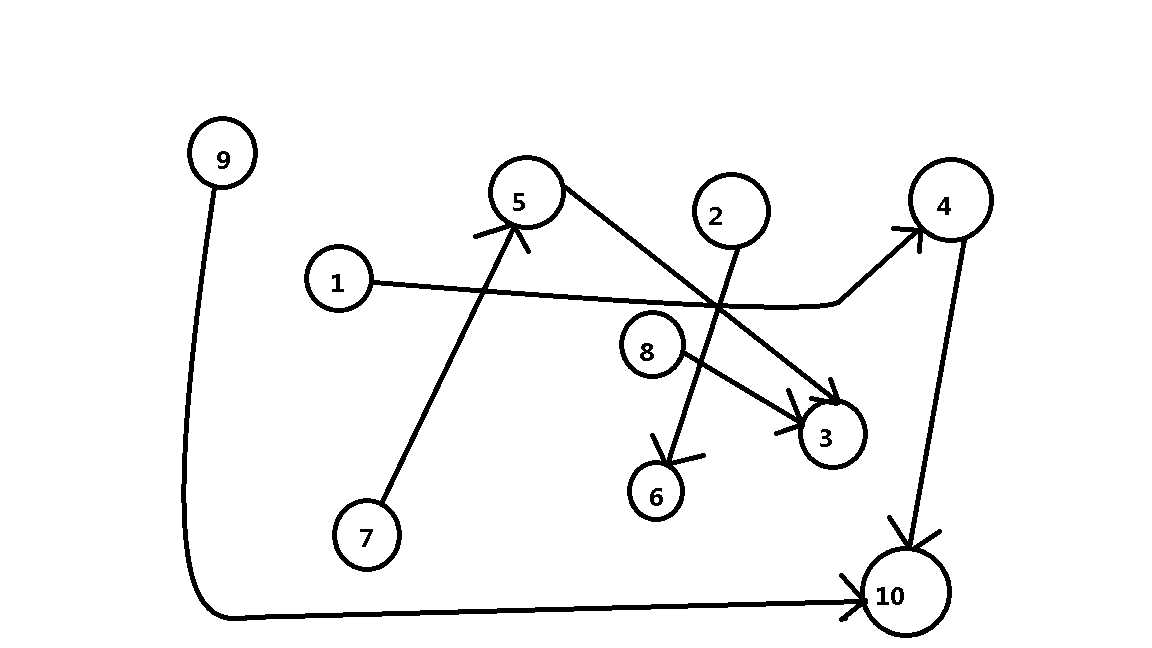
根据图你就可以看出来了点与点之间的关系。//滑稽
合并过程根据
group[get_father(X)]=get_father(Y);这一行代码,这时我们可以模拟一下。在模拟之前,我们先看一下get_father()这一函数。
return (group[x]==x)?x:get_father(group[x]); 这行代码表示查询group[x]里面存的是否为他自身x(主函数内有初始化过group[x]=x,代表每个点的祖宗都是他祖宗),如果存的为自身x,则返回x,代表着祖宗为x,若不是则继续进行递归,继续寻找x的父亲也就是group[x],将x的父亲也就是group[x]再次传入函数,多次找父亲后,如果返回了i则说明x的祖宗为i。
说完了这些,我们来看一下模拟过程。
首先将1,4合并,查询到1的祖宗是1,4的祖宗是4。
所以合并之后把4点当为1的父亲。
再将4,10合并,查询到4的祖宗是4,10的祖宗是10。
所以合并之后把10点当为4的父亲。
再将8,3合并,查询到8的祖宗是8,3的祖宗是3。
所以合并之后把3点当为8的父亲。
再将9,10合并,查询到9的祖宗是9,10的祖宗是10。
所以合并之后把10点当为9的父亲。
再将4,10合并,查询到4的祖宗是4,10的祖宗是10。
所以合并之后把10点当为4的父亲。
再将7,5合并,查询到7的祖宗是7,5的祖宗是5。
所以合并之后把5点当为7的父亲。
再将5,3合并,查询到5的祖宗是5,3的祖宗是3。
所以合并之后把3点当为5的父亲。
再将2,6合并,查询到2的祖宗是2,6的祖宗是6。
所以合并之后把6点当为2的父亲。
这时我们的模拟过程结束,模拟到了上面的图。
所以group[1]=4,group[2]=6,group[3]=3,group[4]=10,group[5]=3,group[6]=6,group[7]=5,group[8]=3,group[9]=10,group[10]。
而查询操作只需要查询他们的祖宗是否是同一祖宗就可以了。
比如查询1和9是否在同一区间。
group[1]-->4 group[4]-->10 group[10]-->10 返回10,说明1的祖宗是10。group[9]=10,group[10]=10。返回10,说明9的祖宗是10。两者的祖宗都是10,则两者在同一区间内。
你以为这就完了吗?不不不,你有没有想过,万一有下图这种可能性呢?
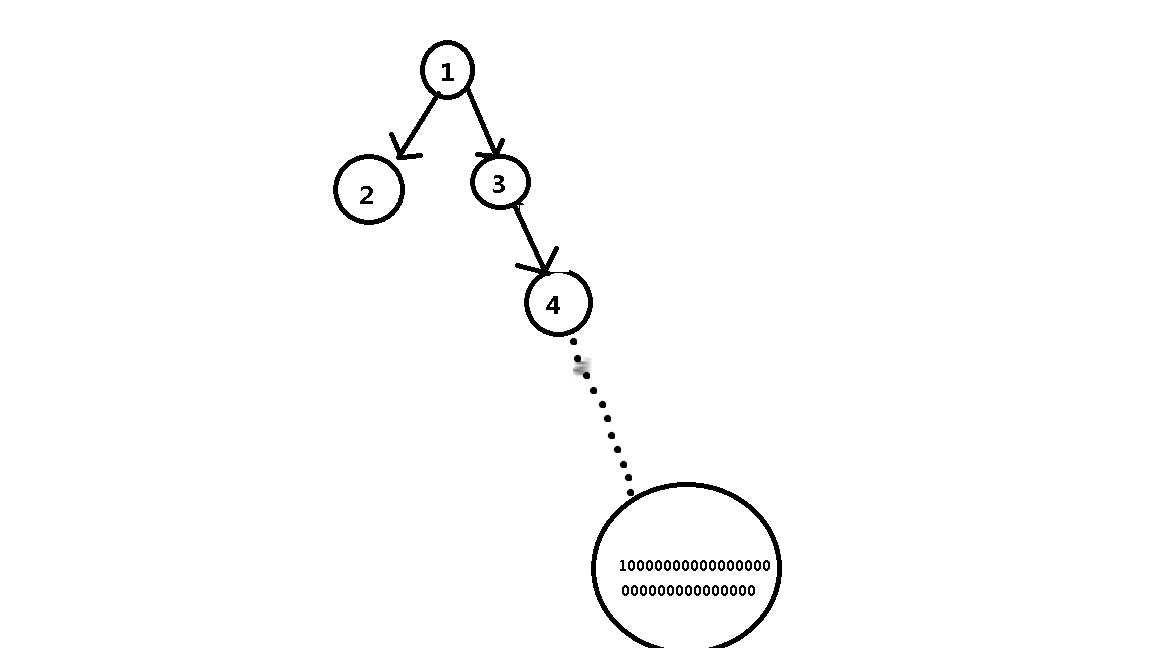
万一他的结构是长长的一条链呢???
众所周知,get_father函数为O(n)为上界的一个函数,那如果像图中的一样,时间复杂度岂不是原地爆炸???
我们必须要对原代码做些什么了。。。。。
我们的优化名字叫做----路径压缩。
我们都知道这行代码是并查集的核心。
return (group[x]==x)?x:get_father(group[x]); 所以我们要在核心上做一些改动。
路径压缩,翻译成人话就是压缩路径(好像没区别,这俩都不是人话)(yyl大佬语录!!!)orz
如果我们将上图中改一点点呢。。。。
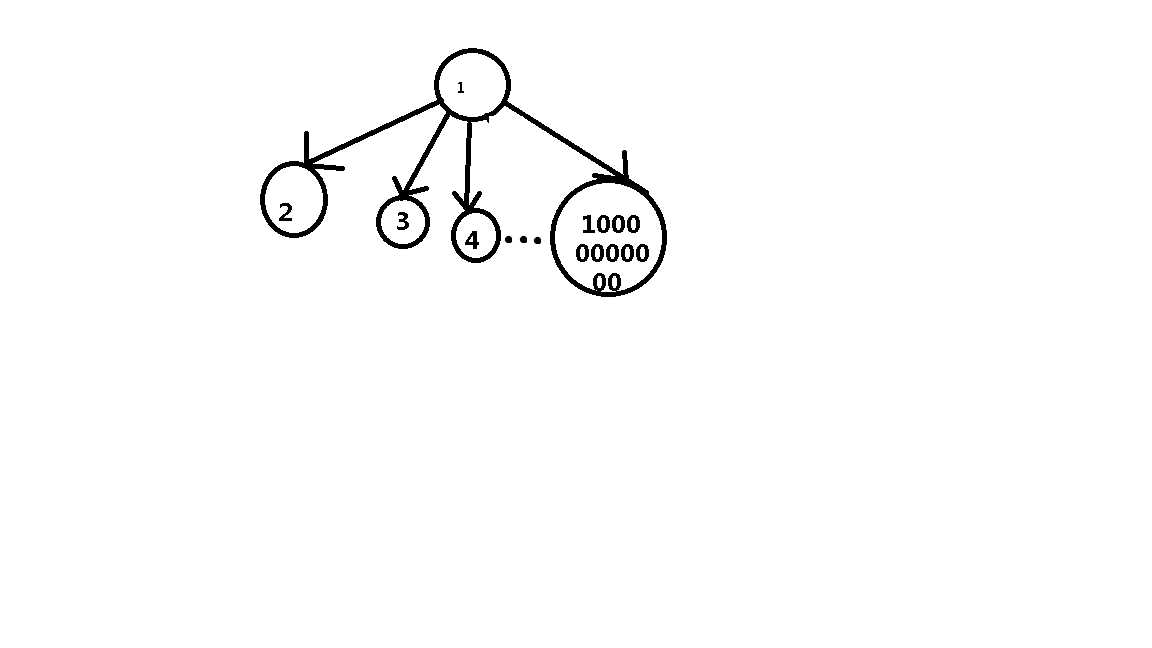
这tm可不是一点点啊。。。不管了不管了
这样,我们将结构改为了上图,那么我们几乎得到了一个时间复杂度为O(1)的查询操作。
可是代码该怎么改???
return (group[x]==x)?x:get_father(group[x]); 我们要将原始代码改为下面的代码
return (group[x]==x)?x:group[x]=get_father(group[x]); 发现有什么不同了没?
没错,我们直接将递归中沿途递归的每个节点的父亲节点直接改指向了这个点的祖宗节点。。。。。
ahhh(惊恐.jpg)
懂了吧,这回我们将代码进行小小的改动可以将时间复杂度降低一大部分(对于主要是长链结构的并查集)。
我们就可以得到上图查询操作时间复杂度为O(1)的操作了。
其实你如果加上读入优化,O(2)(NOIP不让用),直接爽到飞天,亲测从200ms多直接减低为70ms。
数据来源:luogu p3367
原文:https://www.cnblogs.com/zwhwebsite/p/bingchaji.html