POJ1569 ZOJ1704 UVA10112 UVALive5330 Myacm Triangles【点与三角形+最值+暴力】

Myacm Triangles
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 1277 Accepted: 715

Description

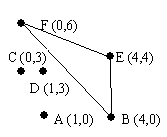
There has been considerable archeological work on the ancient Myacm culture. Many artifacts have been found in what have been called power fields: a fairly small area, less than 100 meters square where there are from four to fifteen tall monuments with crystals on top. Such an area is mapped out above. Most of the artifacts discovered have come from inside a triangular area between just three of the monuments, now called the power triangle. After considerable analysis archeologists agree how this triangle is selected from all the triangles with three monuments as vertices: it is the triangle with the largest possible area that does not contain any other monuments inside the triangle or on an edge of the triangle. Each field contains only one such triangle.

Archeological teams are continuing to find more power fields. They would like to automate the task of locating the power triangles in power fields. Write a program that takes the positions of the monuments in any number of power fields as input and determines the power triangle for each power field.

A useful formula: the area of a triangle with vertices (x1, y1), (x2, y2), and (x3, y3) is the absolute value of

0.5 * [(y3 - y1)(x2 - x1) - (y2 - y1)(x3 - x1)].

Input

For each power field there are several lines of data. The first line is the number of monuments: at least 4, and at most 15. For each monument there is a data line that starts with a one character label for the monument and is followed by the coordinates of the monument, which are nonnegative integers less than 100. The first label is A, and the next is B, and so on.

There is at least one such power field described. The end of input is indicated by a 0 for the number of monuments. The first sample data below corresponds to the diagram in the problem.

Output

For each power field there is one line of output. It contains the three labels of the vertices of the power triangle, listed in increasing alphabetical order, with no spaces.

Sample Input

6
A 1 0
B 4 0
C 0 3
D 1 3
E 4 4
F 0 6
4
A 0 0
B 1 0
C 99 0
D 99 99
0

Sample Output

BEF
BCD

Source

Mid-Central USA 1999

Regionals 1999 >> North America - Mid-Central USA

问题链接：POJ1569 ZOJ1704 UVA10112 UVALive5330 Myacm Triangles
问题简述：（略）
问题分析：
????给定n个坐标点，计算面积最大的由3个点构成的三角形。
????点的数量不多，用暴力法解决，关键是判定三个点构成的三角形内是否有其他点。
程序说明：（略）
参考链接：（略）
题记：（略）

AC的C++语言程序如下：

/* POJ1569 ZOJ1704 UVA10112 UVALive5330 Myacm Triangles */

#include <iostream>
#include <cstdio>
#include <cstdlib>

using namespace std;

const int N = 15;
struct Point {
    char lbl;
    int x,y;
} p[N];

int area(int i, int j, int k)
{
    return abs((p[k].y-p[i].y)*(p[j].x-p[i].x)-(p[j].y-p[i].y)*(p[k].x-p[i].x));
}

bool judge(int i, int j, int k, int n)
{
    for(int x = 0; x < n; x++)
        if(x!=i && x!=j && x!=k)
            if(area(i,j,x) + area(i,k,x) + area(j,k,x) == area(i,j,k))
                return false;
    return true;
}

int main()
{
    int n;
    char lbl[4];
    while(scanf("%d", &n) == 1 && n){
        for(int i = 0; i < n; i++) {
            scanf("%s%d%d", lbl, &p[i].x, &p[i].y);
            p[i].lbl = lbl[0];
        }

        int ii, jj, kk, maxans = -1;
        for(int i = 0; i < n; i++)
            for(int j = 0; j < i; j++)
                for(int k = 0; k < j; k++) {
                    int ans = area(i, j, k);
                    if(judge(i, j, k, n) && ans > maxans)
                        maxans = ans, ii = i, jj = j, kk = k;
                }

        char a = p[ii].lbl, b = p[jj].lbl, c = p[kk].lbl;
        if(a > b) swap(a, b);
        if(b > c) swap(b, c);
        if(a > b) swap(a, b);
        printf("%c%c%c\n", a, b, c);
    }

    return 0;
}

POJ1569 ZOJ1704 UVA10112 UVALive5330 Myacm Triangles【点与三角形+最值+暴力】

原文：https://www.cnblogs.com/tigerisland45/p/10425629.html