RFCN Region Based Fully Connect Network

问题

• 图像分类中的平移不变性（要求）

• 目标检测中的平移变换性（要求）
  ****

  补充FCN

FCN ：全卷积神经网络，去掉CNN最后的全连接层， 从特征中恢复每个像素所属类别（常用于语义分割, 相当于对每个像素进行分类， 用1*1卷积核，即所有像素共用一个分类器）

流程： heatmap -> 反卷积回原图尺寸 -> 11卷积核对像素进行分类
***

感受野计算公式

$$
l_k=l_{k-1}+(f_k-1)\prod_{i=1}^{k-1}s_i
$$
即第k层感受野等于第k-1层的感受野加上jump(本层的kernelsize-1)， jump是之前层的步长的乘积
****

补充各种卷积方法

• 空洞卷积dilate conv, 或者扩张卷积

  

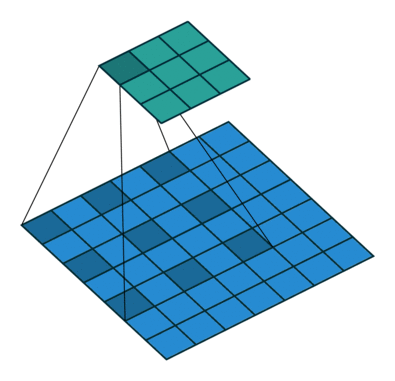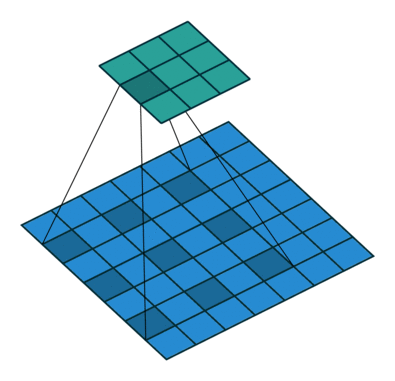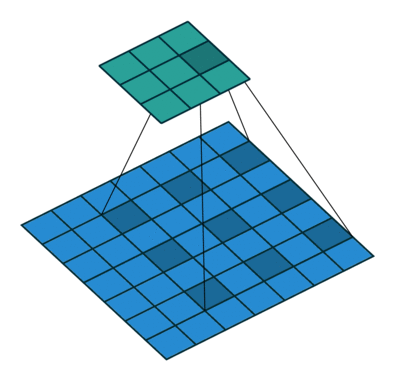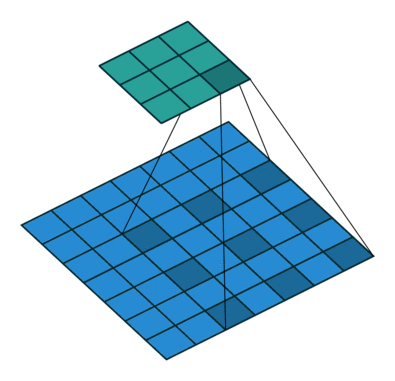
保证卷积核参数不变情况下增加感受野，dilate rate即是kernel之间间隔数量 正常的卷积dilate rate=1

• deconv 或者 transpose conv 转置卷积只能还愿shape 不能还愿value

  input=$\left[ \begin{matrix} x_1 & x_2 & .. & x_4\ .& . &.&. \ .& . &.&. \ .& . &.& x_{16} \\end{matrix}\right]$

  

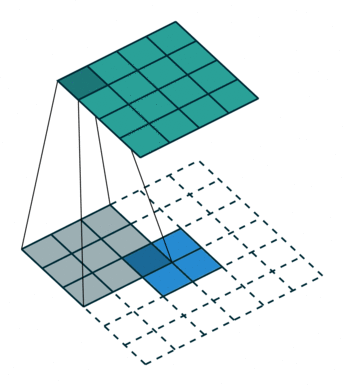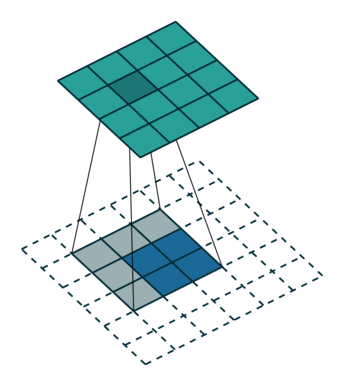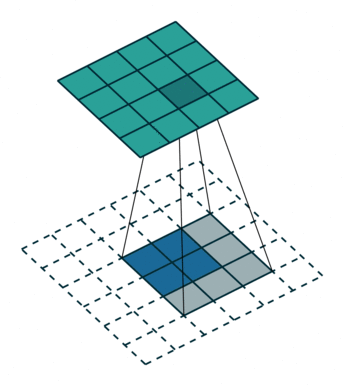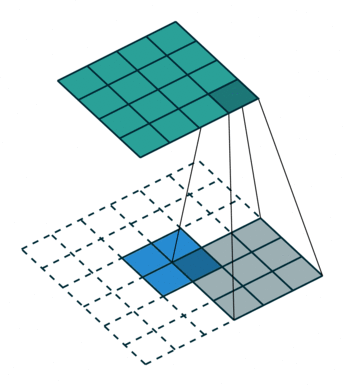
  即进行转置卷积肯定会有padding(即加入的padding使得输出和正常的卷积输入相同)

  i=4, s=1, k=3, $o=\lfloor \frac{i-k+2p}{s} \rfloor+1=2$

  i=2, s=1, k=3, $o=s*(o-1)+k=4$, 在实际实现中需要加入padding(这部分不计入padding)

  记y=Cx， C, x为卷积核， 输入（调整为矩阵形式后的）则

  $\frac{\partial Loss}{\partial x}=\frac{\partial Loss}{\partial y}*\frac{\partial y}{\partial x}=\frac{\partial Loss}{\partial y}{4\times1} \cdot C{16\times4}^T=C^T \cdot \frac{\partial Loss}{\partial y}$

  即正向时左乘C, 反向时右乘$C^T$, 转置卷积是正向左乘$C^T$, 反向时右乘C，因此得名转置卷积

test

原文：https://www.cnblogs.com/mrsihao/p/10424038.html