洛谷P1224 向量内积

时间：2019-02-07 18:09:49 阅读：191 评论：0 收藏：0 [点我收藏+]

什么毒瘤......

题意：给定n个d维向量，定义向量a和b的内积为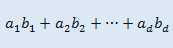技术分享图片

求是否存在两个向量使得它们的内积为k的倍数，并给出任一种方案。k <= 3。

解：很容易想到一个暴力是n²d的。显然我们不能n²枚举，所以要一次性把一个向量跟多个向量判断。

先思考k = 2的情况，显然每个位置和内积非0即1，这启发我们使用二进制。

假如把一个内积看成一个B进制数或者一个多项式，变量是B，我们就能发现，如果两个向量的内积为x，那么这个多项式的值也是x。

这种情况只要B取一个奇数就行了。理由是内积每一项非0即1，而进制为奇数的话，每一项的xⁱ % 2 = 1，奇偶性不变。所以最后加起来和直接加起来的奇偶性相同。

k = 3的时候只要进制为3a + 1就行了。所以最终我们选择7进制。

然后有个很严峻的问题：我们要找一个运算使之与按位乘相对应。先想到了转成指标加法，经过一番推倒之后发现不可行。然后陷入江局......

正解：再观察一波内积式子，您就会发现这个其实是矩阵乘法中的一个位置的计算式......反正我是没发现。

那么令A = n × d的矩阵，B = A * A^T，则B_i,j就是i和j的内积。

然后我们只需检验B和全1矩阵(对角线不一定是1)是否相同即可。这有一个经典算法：随机向量法。

随机出来的向量哪一位不同，就表明在全1矩阵的哪一列中存在差异。枚举跟这个向量匹配的向量即可。

k = 3的时候，我们把B中每一个元素都取平方，这样1和2都会变成1。

那么怎么把B中的每个元素取平方呢？

把B中某个元素的式子化开，会有：

技术分享图片

然后就做完了......

  1 #include <cstdio>
  2 #include <algorithm>
  3 #include <ctime>
  4 #include <iostream>
  5 
  6 const int N = 100010;
  7 
  8 int a[N][110], now[N], C[N], D[N], E[N], MO, F[N];
  9 int n, d;
 10 
 11 inline bool check(int i, int j) {
 12     int ans = 0;
 13     for(int k = 1; k <= d; k++) {
 14         (ans += a[i][k] * a[j][k]) %= MO;
 15     }
 16     return ans;
 17 }
 18 
 19 inline void solve1() {
 20     int T = 5, f = -1;
 21     while((T--) && (f == -1)) {
 22         int Sum = 0;
 23         for(int i = 1; i <= n; i++) {
 24             C[i] = rand() & 1;
 25             Sum += C[i];
 26         }
 27         //mul(1, n, d, C, a, D);
 28         for(int i = 1; i <= d; i++) {
 29             D[i] = 0;
 30             for(int j = 1; j <= n; j++) {
 31                 D[i] += C[j] * a[j][i];
 32                 D[i] &= 1;
 33             }
 34         }
 35         //mul(1, d, n, D, aT, E);
 36         for(int i = 1; i <= n; i++) {
 37             E[i] = 0;
 38             for(int j = 1; j <= d; j++) {
 39                 E[i] += D[j] * a[i][j];
 40                 E[i] &= 1;
 41             }
 42         }
 43         //mul_one(1, n, n, C, F);
 44         for(int i = 1; i <= n; i++) {
 45             F[i] = ((Sum - C[i]) + C[i] * now[i]) & 1;
 46             if(E[i] != F[i]) {
 47                 f = i;
 48                 break;
 49             }
 50         }
 51     }
 52     if(f == -1) {
 53         printf("%d %d\n", f, f);
 54         return;
 55     }
 56     for(int i = 1; i <= n; i++) {
 57         if(i == f) {
 58             continue;
 59         }
 60         if(!check(i, f)) {
 61             printf("%d %d\n", std::min(i, f), std::max(i, f));
 62             return;
 63         }
 64     }
 65     return;
 66 }
 67 
 68 inline void solve2() {
 69     int T = 5, f = -1;
 70     while((T--) && (f == -1)) {
 71         int Sum = 0;
 72         for(int i = 1; i <= n; i++) {
 73             C[i] = rand() % MO;
 74             Sum += C[i];
 75         }
 76         //mul(1, n, d, C, a, D);
 77         for(int i = 1; i <= d; i++) {
 78             for(int ii = 1; ii <= d; ii++) {
 79                 int pos = (i - 1) * d + ii;
 80                 D[pos] = 0;
 81                 for(int j = 1; j <= n; j++) {
 82                     D[pos] += C[j] * a[j][i] * a[j][ii];
 83                     D[pos] %= MO;
 84                 }
 85             }
 86         }
 87         //mul(1, d, n, D, aT, E);
 88         for(int i = 1; i <= n; i++) {
 89             E[i] = 0;
 90             for(int j = 1; j <= d; j++) {
 91                 for(int jj = 1; jj <= d; jj++) {
 92                     int pos = (j - 1) * d + jj;
 93                     E[i] += D[pos] * a[i][j] * a[i][jj];
 94                     E[i] %= MO;
 95                 }
 96             }
 97         }
 98         //mul_one(1, n, n, C, F);
 99         for(int i = 1; i <= n; i++) {
100             F[i] = ((Sum - C[i]) + C[i] * now[i]) % MO;
101             if(E[i] != F[i]) {
102                 f = i;
103                 break;
104             }
105         }
106     }
107     if(f == -1) {
108         printf("%d %d\n", f, f);
109         return;
110     }
111     for(int i = 1; i <= n; i++) {
112         if(i == f) {
113             continue;
114         }
115         if(!check(i, f)) {
116             printf("%d %d\n", std::min(i, f), std::max(i, f));
117             break;
118         }
119     }
120     return;
121 }
122 
123 int main() {
124     srand(time(0));
125     int k, x;
126     scanf("%d%d%d", &n, &d, &k);
127     MO = k;
128     bool f = (k == 2);
129     for(int i = 1; i <= n; i++) {
130         now[i] = 0;
131         for(int j = 1; j <= d; j++) {
132             scanf("%d", &x);
133             a[i][j] = x % k;
134             now[i] += a[i][j] * a[i][j];
135         }
136         now[i] %= k;
137     }
138 
139     f ? solve1() : solve2();
140     return 0;
141 }

AC代码

题解里还有一种神奇的解法，使用了乘法分配率，每次把一个向量和它上面所有向量的乘积加起来跟(i-1) % MO判断。

分配一下，就是把上面向量的每一维都做前缀和，然后相乘。

这样做其实有一点问题，就是可能有乘积为0的检测不出来。不过上面那种方法也彼此彼此了。

洛谷P1224 向量内积

原文：https://www.cnblogs.com/huyufeifei/p/10355016.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)