扩展欧几里得算法

定义：

贝祖定理对于任意整数a,b，存在一对整数x,y,满足ax+by=gcd(a,b)

用欧几里得算法计算一组x,y的方法，称作“扩展欧几里得”算法

求解

思路

假设a>b
\[ (1) b=0:gcd(a,b)=a,ax+by=a,则x=1,y=0; \]

\[ (2)b\neq0，如图 \]

Code

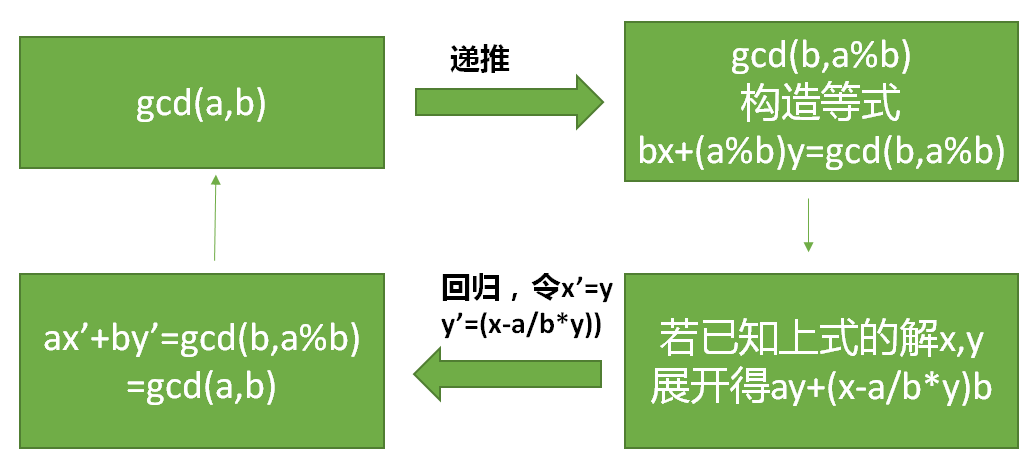
int exgcd(int a,int b,int &x,int &y){//求解ax+by=gcd(a,b)x,y 并返回 最大公约数 
    if(b==0){
        x=1,y=0;
        return a;
    }
    int d=exgcd(b,a%b,x,y);
    int tmp=x;x=y;y=tmp-(a/b)*y;
    return d;
}

一般

对于ax+by=c 该方程有解当且仅当

gcd(a,b)|c

此时可先求ax+by=gcd(a,b)的解x‘,y‘,即ax‘+by‘=gcd(a,b),令d=gcd(a,b),等式两边同时乘以c/d可得原方程的一组解为：
\[ \left\{\begin{matrix}x={x}'\cdot c/d \\ y={y}'\cdot c/d \end{matrix}\right. \]
Ps:通解
\[ \left\{\begin{matrix}x={x}'\cdot \frac{c}{d}+k\frac{b}{d} \\ y={y}'\cdot \frac{c}{d}-k\frac{a}{d} \end{matrix}\right. \]
?通解说明：

?ax+by=c，令a(x+t1)+b(y+t2)=c，可得

?at1=-bt2，左右两边必须同时包含a,b的因子

?最小的满足上式的正整数为lcm(a,b)

?即at1=-bt2=k*lcm(a,b)

?则t1=klcm(a,b)/a=kb/gcd(a,b)

? t2=…=-k*a/gcd(a,b)

扩展欧几里得算法

原文：https://www.cnblogs.com/saitoasuka/p/10335922.html