目录
目前自己学习中存在的薄弱的知识点具体有哪些?每个薄弱的知识点都是如何获知的,每个薄弱的知识点需要列举具体的例子说明。(5分)
一 :相对而言,对于字符串的操作应该还存在不足。例如,自己编写字符串处理函数(strlen, strcpy, strcat以及strcmp) 并不能做到非常地熟练。在此过程中,也出现过一些错误。
例如:①输入时未注意到字符串中地分隔符,因此获取失败。因此,需要特别的处理技巧。②忽略字符串末尾地“\0”结束符,经常忘记在结尾补充\0,导致一些未能预料地错误。
对于这个,书本给出了
strcpy的例子,我仿照了这个例子,去分别用指针方式和数组方式,实现这几个操作。对于strcmp这个不太熟悉如何写的,我阅读了库函数的代码,大致了解了它的思路。它的思路是,用指针下移的方法,查看两者字符是否出现\0,如果是,则结束。并且,下移的过程中,持续比较两者的 ACSII 码,按照0, -1, 1的方式返回结果值。
二 :数组的交并补集。我认为这是一个难点。以求对称差集为例。在求解的过程中还需要数组原有的顺序不变。这是出现在中段测试中的一道题目。在当时,我是没有什么思路的。后来,我发现这就是一个数学问题:求对称差集。对于我个人,我想出了一种算法,大致思路如下:就是先分别查找并去除两个数组内部的重复元素,然后求出交集,再分别用处理后的数组去除交集中的元素,即可实现。
这一项我在第二项中将详细阐述。
三 :矩阵转置循环。这个并不算薄弱的知识点。但的确可以作为一个有趣的典例来学习。因为其循环的开始下标并不是0,这是观察矩阵转置的规律后就能够得出的。如果盲目的整个矩阵进行处理,反而可能出现问题。所以,我们仅需对左下角和右上角进行循环操作即可。
这个目前参考了书本119页的例子,并且结合了线代的知识作了一些思考,避免了将整个矩阵进行操作的误区。
[x] 矩阵转置
从第五章函数到第七章数组的函数题和编程题(主要是在PTA)中选出至少一道你觉得比较有挑战的题(已解决且不是奇奇的题)。写出解题报告包括:
(1)题目大意;
(2)解题思路;
(3)代码思路,比如画出流程图;
(4)核心技术总结;
(5)解题过程中存在的问题,以及如何得到解决的。(5分)
除去奇奇哥的题目,我挑选了两道题目在此列出。
一道是上述中段测试的一道求对称差集的题目,另一道则是扫描出最长单词。
给定两个整型数组,本题要求找出不是两者共有的元素。
输入分别在两行中给出两个整型数组,每行先给出正整数N(≤20),随后是N个整数,其间以空格分隔。
在一行中按照数字给出的顺序输出不是两数组共有的元素,数字间以空格分隔,但行末不得有多余的空格。题目保证至少存在一个这样的数字。同一数字不重复输出。
10 3 -5 2 8 0 3 5 -15 9 100
11 6 4 8 2 6 -5 9 0 100 8 13 5 -15 6 4 1先遍历a数组,将其与b数组比较,将a数组中不同的元素放到c数组中暂存。
然后对c数组进行一次查重去重。
再遍历b数组,将其与a数组比较,将b数组中不同的元素放到c数组中暂存,然后对c数组进行第二次查重去重。
输出c数组。
流程图如下:
st=>start: Start
e=>end
op1=>operation: 遍历a数组并与b数组比较
op2=>operation: 结果存到c数组
op3=>operation: 对c数组查重
op4=>operation: 遍历b数组并与a数组比较
op5=>operation: 结果存到c数组
op6=>operation: 输出c数组
cond=>condition: 是否有重复元素
cond2=>condition: 是否有重复元素
cond1=>condition: 是否有重复元素
op7=>operation: 去重
st->op1->op2->op3->cond
cond(yes)->op7->cond->
cond(no)->op4->op5->op3->cond1
cond(yes)->op7->cond1->e
cond2(no)->op6->e最本质的需求,就是明确其中的数学本质,我们可以这样去理解,我们是在求这两个集合交集的补集。这在数学上又被称为对称差集。
由此,我引出了另一个思路。是否有一个函数,可以直接求出对称差集。查阅std库函数,的确有。因此思路2即使用该函数求解。
代码的核心部分:
for (j = 0; j < n1; j++)
{
flag = 0;
for (i = 0; i < n2; i++)
{
if (a[j] == b[i]) flag = 1;
}
if (flag == 0)
{
int k, flag1 = 0;
for (k = 0; k <= count; k++)
{
if (c[k] == a[j]) {
flag1 = 1;
}
}
if (flag1 == 0)
{
c[count] = a[j];
count++;
}
}
}在这里,我想放出几种集合的关系图:
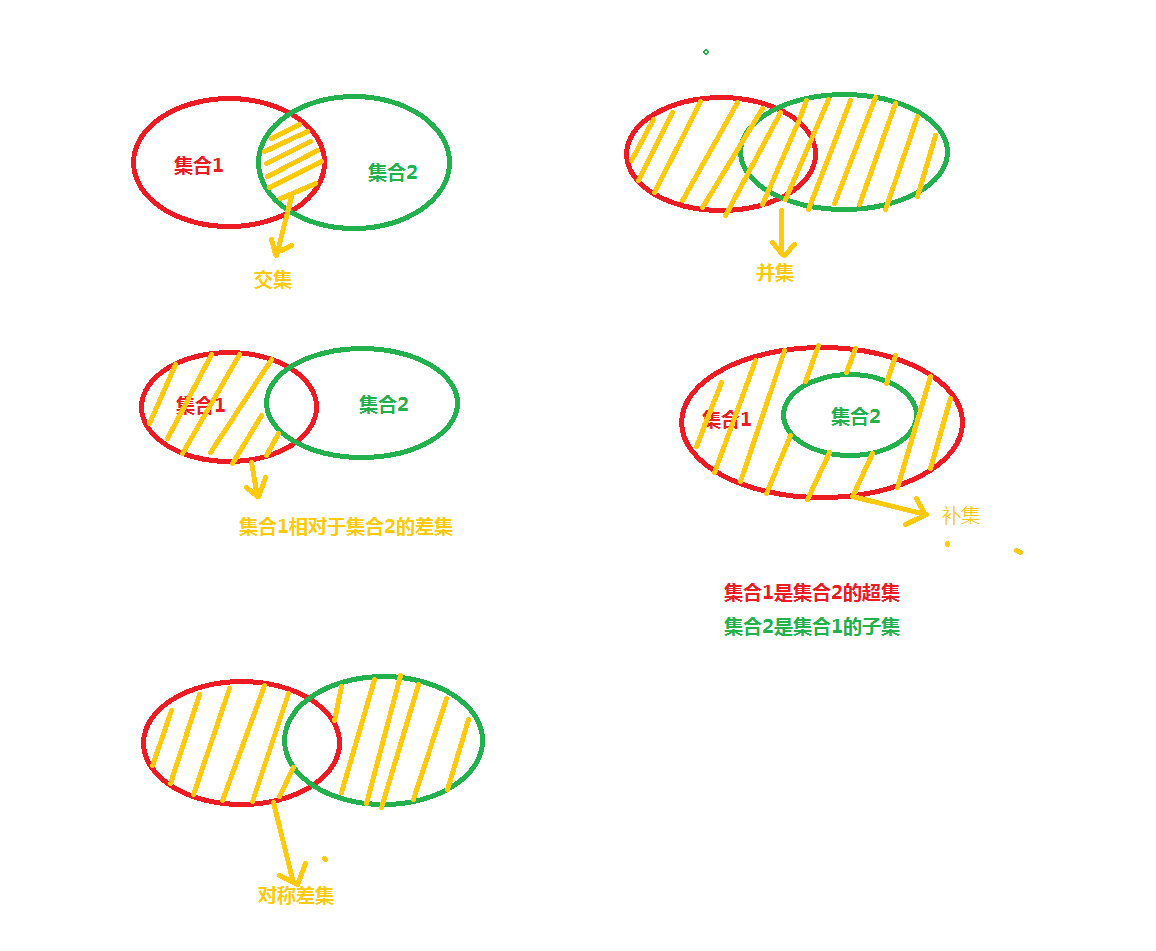
直接采用求对称差集的函数。简单快捷高效。
std::set_symmetric_difference(str1, str2)
另外几种集合的库函数如下:
set_unoin(求并集)
set_intersection(求交集)
set_difference(求差集)
set_symmetric_difference(求对称差集)
在主函数中输入一个字符串main_str,调用函数将main_str中最长的单词取出放入sub_str中(要求被调函数参数为main_str和sub_str),在主函数中输出结果字符串sub_str。假定输入的字符串main_str中单词以一个或多个空格分开。若有多个单词长度相同,输出最后一个。要求函数用指针变量作形参。
一个字符串,串中单词以一个或多个空格分开。
输出字符串中最长的单词。
在这里给出一组输入。例如:
She is a nice girl.在这里给出相应的输出。例如:
girl.遍历字符数组,然后参考教材中xx页的例子,运用跳过连续空格的技术。并且认为,句子于第一个’\0’出现时结束。设置一个flag,统计单词长度,并将每一次的最长单词与长度存放到str3和k中。在遍历数组的过程中不断比较,直至最后,得到正确的结果。
流程图如下:
st=>start: 开始
e=>end: 结束
st=>start: Start
e=>end
op1=>operation: 遍历数组
op2=>operation: 结果存到c数组
op3=>operation: 检查下一字符
op4=>operation: 单词长度+1
cond=>condition: 是否有空格
st->op1->cond
cond(yes,left)->op3->e
cond(no)->op4->op3->e
代码的核心部分:
for (int i = 0; i <= strlen(str1); i++)
{
count++;
if (str1[i] == ‘ ‘ || str1[i] == ‘\0‘)
{
if (count >= max)
{
max = count;
point = i;
}
count = 0;
}
}
for (int i = point - max + 1; i < point; i++)
{
*(str2 + j) = *(str1 + i);
j++;
}
str2[j] = ‘\0‘;
}这里再简要提一下矩阵转置吧。
矩阵转置的核心在于弄懂转置的原理!!!
即沿对角线对称元素的互换
void transpose(int a[][4])
{
for (int i = 0; i < 4; i++)
{
for (int j = i + 1; j < 4; j++) //注意这里的j的初值,因对上三角处理,j=i+1
{
int t = a[i][j];
a[i][j] = a[j][i];
a[j][i] = t;
}
}
}这里 j 的初值设置得比较特殊,值得注意。
原文:https://www.cnblogs.com/cube-north/p/10088019.html