20172319 2018.11.04-11.11

《程序设计与数据结构》第8周学习总结

目录

• 教材学习内容总结
• 教材学习中的问题和解决过程
• 代码调试中的问题和解决过程
• 代码托管
• 上周考试错题总结
• 结对及互评
• 学习进度条
• 参考资料

教材学习内容总结

第十二章 优先队列与堆

• 12.1?堆：

• 堆（heap） ： 具有两个附加属性 的二叉树；是一棵完全二叉树。

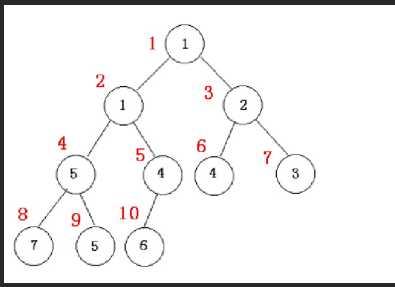
• 最小堆（minheap） ： 每一结点小于或等于其两个孩子；其根的两个孩子同样为最小堆。
  

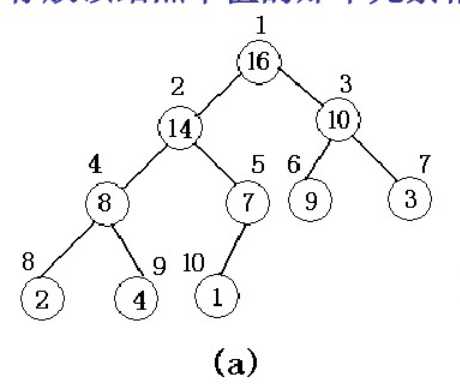
• 最大堆（maxheap） ： 每一结点大于或等于其两个孩子；其根的两个孩子同样为最大堆。
  

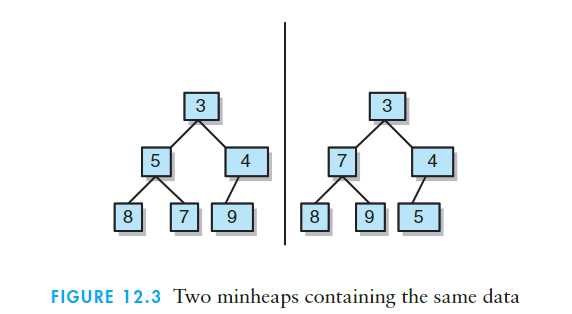
• 元素相同，构造的堆也可以不同：
  

• 堆的操作 ：

• 操作	说明
  addElement	将给定元素添加到该堆中
  removeMin	删除堆的最小元素
  findMin	返回一个指向堆中最小元素的引用

• 11.2?用链表实现二叉查找树

• 11.2.1?addElement操作：

• 1.若树为空，新元素成为根结点；
• 2.若树非空，新元素与树根元素进行比较：
• （1）若其小于根结点存储的元素：
• 若左孩子为空，新元素成为根的左孩子；若左孩子不为空，则遍历根的左孩子，再次进行比较操作。
• （2）若其大于或等于根结点存储的元素：

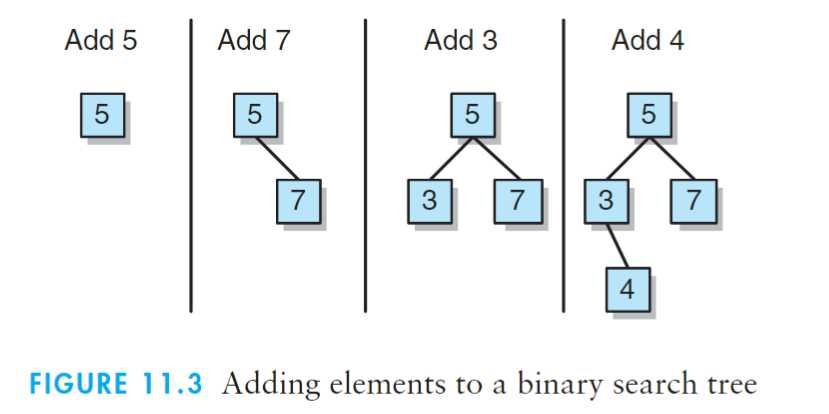
• 若右孩子为空，新元素成为根的右孩子；若右孩子不为空，则遍历根的右孩子，再次进行比较操作。

• 11.2.2?removeElement操作：
  

• 必须要推出 另一个结点来代替要被删除的那个结点。
• 用protected封装的replacement方法返回指向一个结点的引用，该结点将代替要删除的结点。
• 选择替换结点的三种情况如下：
• 1.若被删除结点无孩子，则replacement返回null；
• 2.若被删除的结点只有一个右孩子，则replacement返回此孩子；

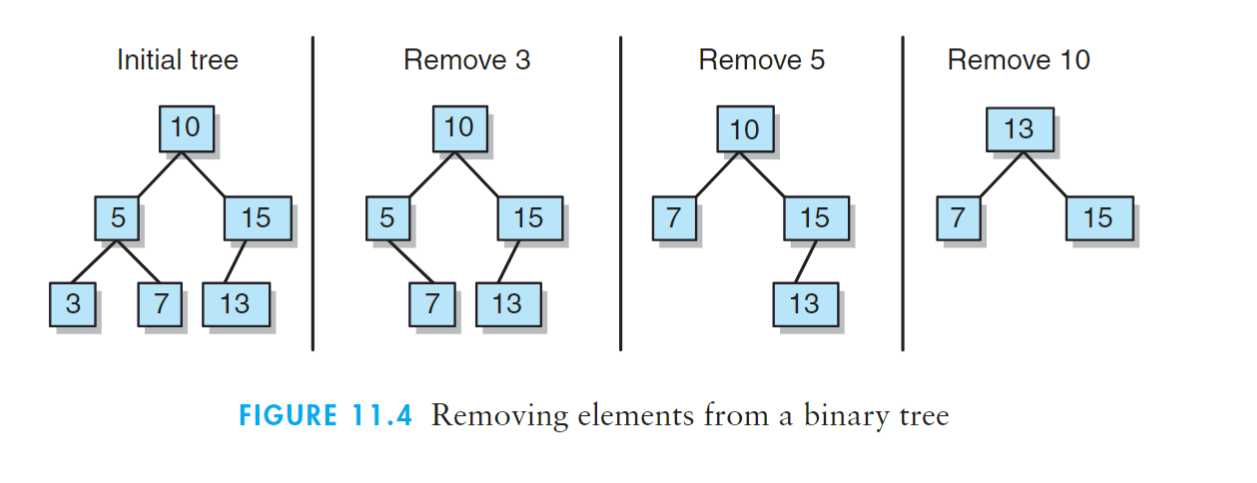
• 3.若被删除的结点有两个孩子，则replacement返回中序遍历中的后继者。

• 11.2.3?removeAllOccurrences操作：

• 反复调用removeElement方法来删除某一指定元素的所有存在。

• 11.2.4?removeMin操作：
  

• 最小元素在二叉查找树中的三种可能情形：
• 1.若根无左孩子，则其为最小元素，而其右结点会变成新的根结点；
• 2.若树的最左侧结点是一片叶子，则这片叶子就是最小元素，只需设置其父节点的左孩子为null即可；

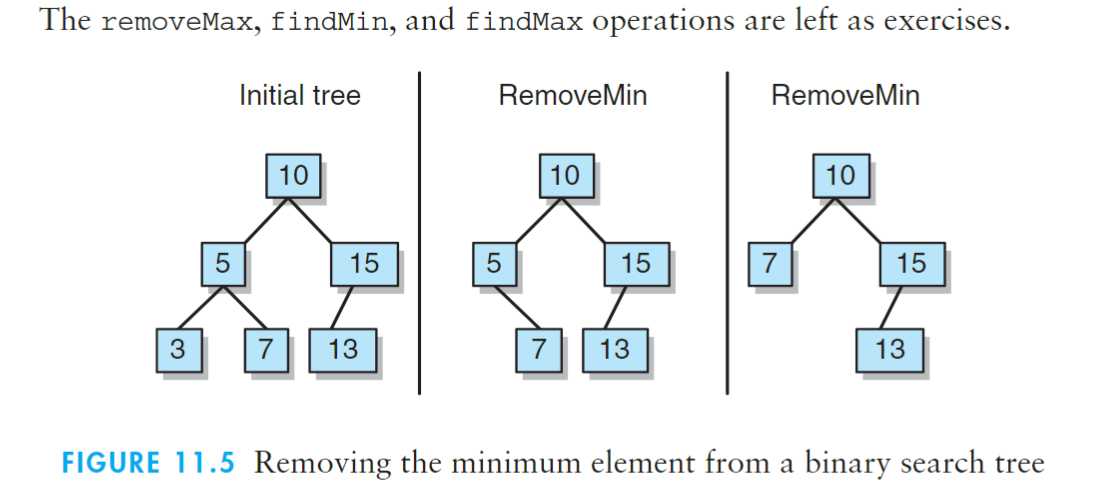
• 3.若树的最左侧结点是一个内部结点，则需要设置其父结点的左孩子引用指向这个将删除结点的右孩子。

• 11.3?用有序列表实现二叉查找树

• 列表的一些常见操作：

• 操作	描述
  removeFirst	从列表中删除第一个元素
  removeLast	从列表中删除最后一个元素
  remove	从列表中删除某个元素
  first	查看位于列表前端的元素
  last	查看位于列表末端的元素
  contains	确定列表是否含有某一个元素
  isEmpty	判定列表是否为空
  size	确定列表中的元素数量

• 有序列表的特有操作：

• 操作	描述
  add	向列表中添加一个元素

• 11.3.1?BinarySearchTree实现的分析：

• 在BinarySearchTreeList实现中用到的LinkedBinarySearchTree实现是一种具有附加属性的平衡二叉查找树；
• 附加属性：假设树中存储的元素数目是n，则任何结点的最大深度为log₂ⁿ。
• 有序列表的链表实现分析和二叉查找树实现分析：

• 操作	LinkedList	BinarySearchTreeList
  removeFirst	O（1）	O（log n）
  removeLast	O（n）	O（log n）
  remove	O（n）	O（log n）*
  first	O（1）	O（log n）
  last	O（n）	O（log n）
  contains	O（n）	O（log n）
  isEmpty	O（1）	O（1）
  size	O（1）	O（1）
  add	O（n）	O（log n） *
  add操作和remove操作都可能导致树变得不平衡

• 11.4?平衡二叉查找树
  
• 只有保持平衡，二叉树的查找效率才会高。
• 实现目的：保持树的最大路径长度趋近于：log₂ⁿ。
• 锐化树（degenerate tree） ：
  

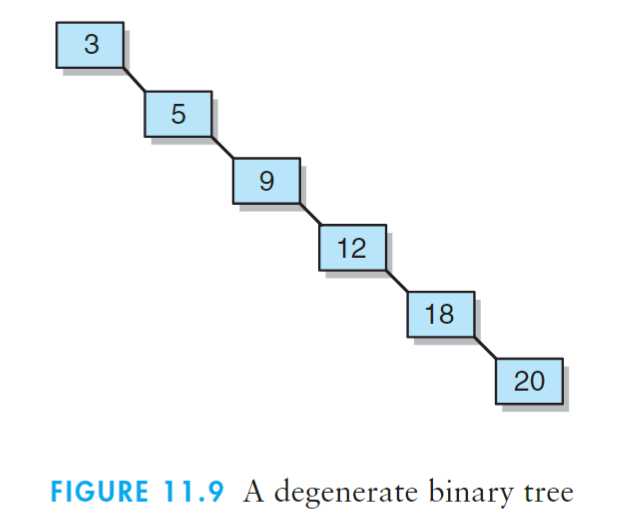
• 其看起来更像是一个链表，然而其效率却比链表还低，其附带了额外的开销。

• 若无平衡假设，则最坏情况下addElement操作的时间复杂度为O（n）而不是O（log n），树根是最小元素，而即将被插入的元素可能成为树中的最大元素。

• 11.4.1?右旋（right rotation）：
  

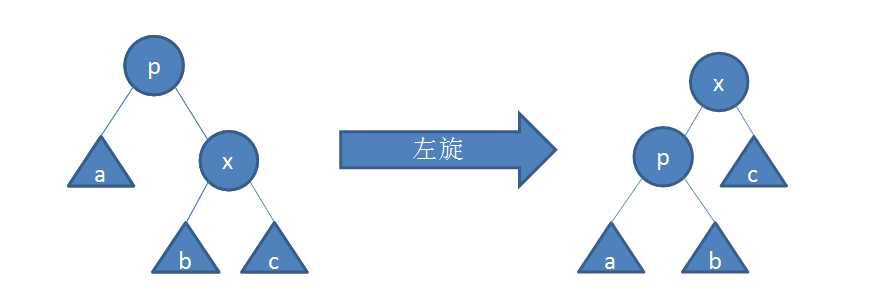
• 左孩子绕着其父结点向右旋转；
  

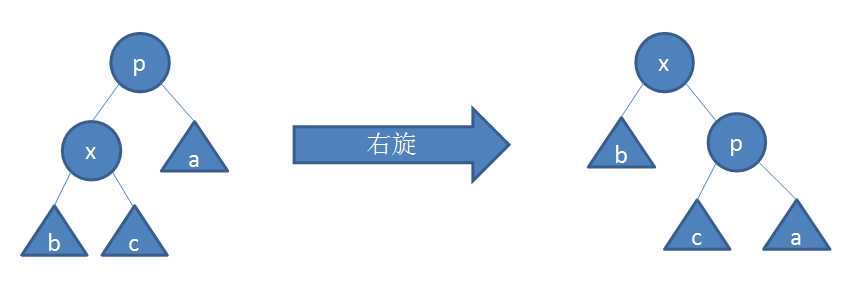
• 旋转前，x是p的左儿子。x的右儿子（若存在）变为p的左儿子，p变为x的右儿子。

• 11.4.2?左旋（left rotation）：
  
• 右孩子绕着其父结点向左旋转；
  

• 旋转前，x是p的右儿子。x的左儿子（若存在）变为p的右儿子，p变为x的左儿子。

• 许多时候，一棵不平衡树要趋近平衡所需要的旋转不止一次。

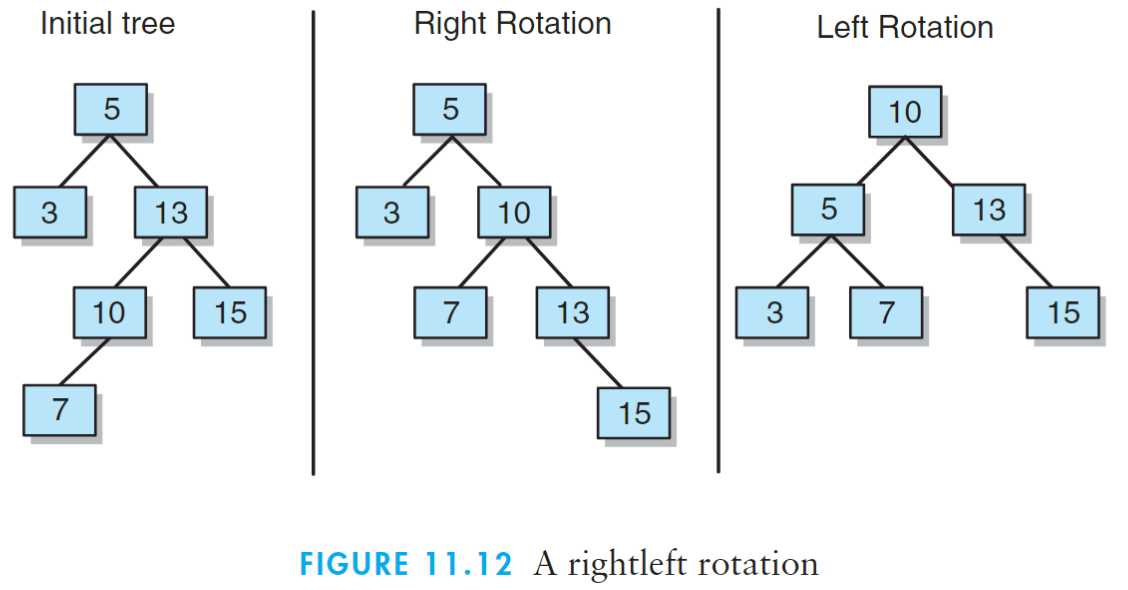
• 11.4.3?右左旋（rightleft rotation）：
  

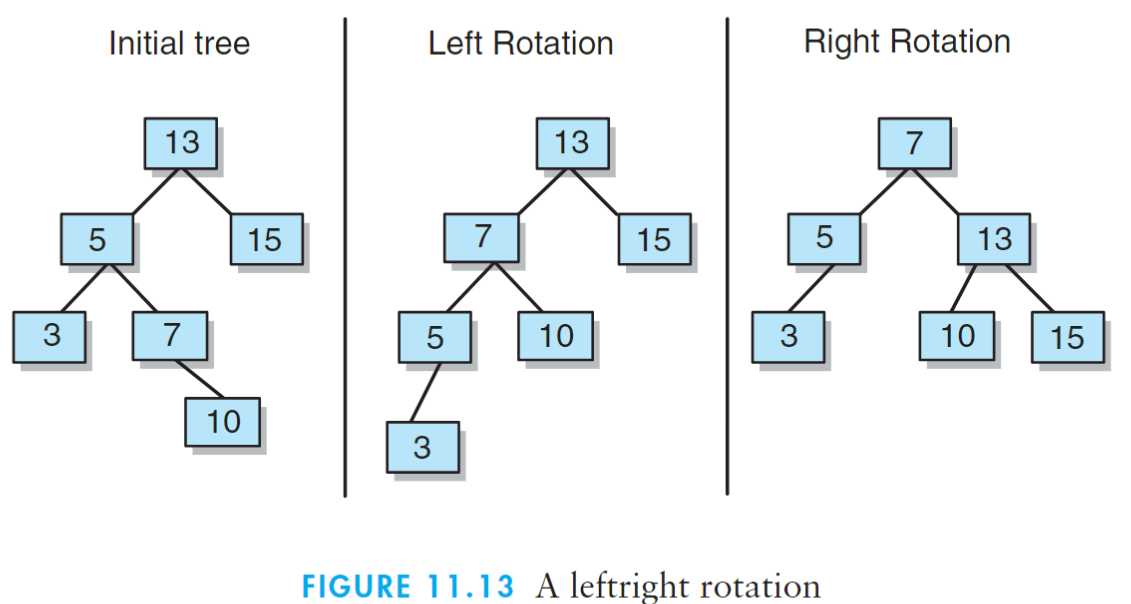
• 11.4.3?左右旋（leftright rotation）：

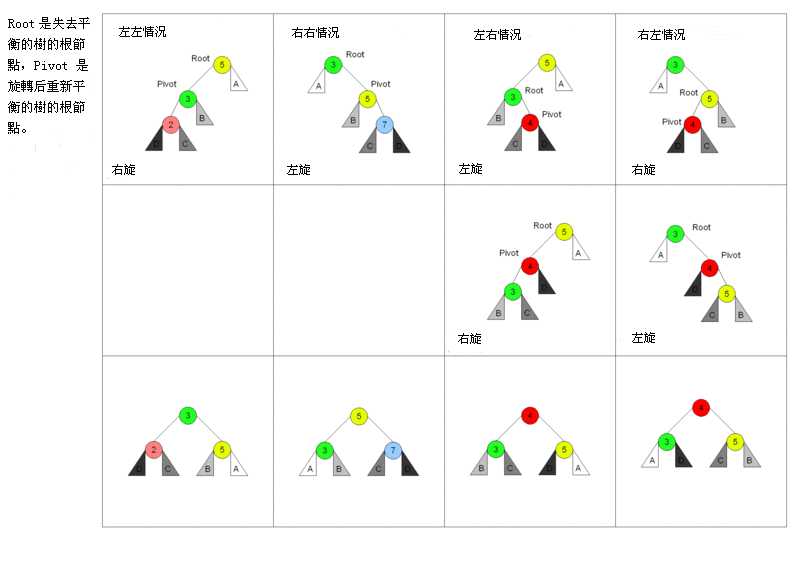
• 11.5?实现二叉查找树：AVL树

• 一种高度平衡的二叉查找树，其能尽可能地降低树的高度，以此减少树的平均查找长度。
• 性质：
• 1.左右子树高度差的绝对值不超过1 ；
• 2.树中的每个子树都是AVL树；

• 3.每个节点都有一个平衡因子(balance factor),任一节点的平衡因子是-1,0,1。(每个节点的平衡因子等于右子树的高度减去左子树的高度 )
  

• 11.6?实现二叉查找树：红黑树

返回目录

教材学习中的问题和解决过程

• 问题1：2-3-4树？
• 解决：

返回目录

代码调试中的问题和解决过程

• 问题1：如何删除某一指定结点的子树。

• 解决：

返回目录

代码托管

返回目录

上周考试错题总结

• 错题1：上周无测试活动。
• 解决：
• 错题2：
• 解决：
• 错题3：
• 解决：

返回目录

结对及互评

点评过的同学博客和代码

• 本周结对学习情况：
  • 20172316赵乾宸
    
  • 博客中值得学习的或存在问题：
    
  • 20172329王文彬
    
  • 博客中值得学习的或存在问题：
  • 博客内容充实、排版整齐、对教材内容有经过一番认真思考、继续保持。
  • 代码截图做标注时应尽量避免遮挡代码。
  • Markdown的部分缩进有误。
  • 教材问题2提出得很好，可以看出近断时间来反复使用链表、数组去实现同一类型的数据结构起得了一定的成效。

返回目录

学习进度条

返回目录

参考资料

• 二叉搜索树的平衡--AVL树和树的旋转（图解）
• 清晰理解红黑树的演变---红黑的含义
• 二叉查找树中的插入查找和删除
  返回目录

20172319 《程序设计与数据结构》 第八周学习总结

原文：https://www.cnblogs.com/Tangcaiming/p/9940677.html