逻辑回归案例

小细节

• 逻辑回归（logistic regression）虽然被称之为逻辑回归，但是它本质上其实是一种分类算法（classification algorithm），逻辑回归名字的由来是有历史原因的。
• sigmoid函数在逻辑回归中站着重要的位置，sigmoid function也被称为logistic function，称之为逻辑函数就做到了见名知意了，说明\({{1}\over{1 + e^{-x}}}\)与逻辑回归密切相关。
• 在线性回归中得知，假设函数\(h(x) = \theta_0 + \theta_1x\)，逻辑回归处理的是分类的问题，那么我们的算法要么输出的是概率（返回在0到1之间），要么是输出的就是0或者1等等，在线性回归中建立的假设函数\(h(x) = \theta_0 + \theta_1x\)显然不会在0到1之间或者输出的值为0或者1，这个时候就需要sigmoid函数了；sigmoid函数可以将实数范围内的值转换为0-1之间的值，而这个值恰巧就是概率所在的范围，进一步的，得到了概率的值，只要我们设定了阈值（threshold）就可以将其转换为0或者1等等。
• 逻辑回归是在线性回归的基础上发展而来的，它是依赖于线性回归的，为什么？因为在逻辑回归中，定义的假设函数时\(h_{\theta}(x) = g(\theta^{T}x)\)，其中\(\theta^{T}x\)就是在线性回归中假设函数的矩阵形式，在逻辑回归中通过g函数将其封装到sigmoid函数中，\(g(x) = {{1} \over {1 + e^{-x}}}\)，只有这样，才能将\(\theta^{T}x\)这个输出在R上的值映射到0-1之间，所有逻辑回归中的假设函数为\(h_{\theta}(x) = g(\theta^{T}x) = {{1} \over {1 + e^{-\theta^{T}x}}}\)。
• 逻辑回归假设函数的概率表现形式: \(h(x) = g(\theta^{T}x) = P(y = 1|x; \theta)\)，在提醒一下，这里的\(\theta\)是一个列向量，在MATLAB/Octave中出现公式的地方，十有八九都是使用矩阵方程表达的，输入和输出也大部分是列向量或者矩阵。
• 关于阈值（threshold），在上面几点中已经提到的，这里提一下如何将一个0-1的概率值转换为一个0或者1等等的分类结果，首先根据通过sigmoid函数，我们的线性回归的结果会被锁定到0-1之间，这个时候如果假设函数\(h_{\theta}(x) = g(\theta^{T}x) = {{1} \over {1 + e^{-\theta^{T}x}}}\)的结果为0.7，表示 \(y = 1\)的概率为0.7，对立的，\(y = 0\)的概率为0.3，如果规定threshold为0.5，则表示如果假设函数\(h()\)的输出大于等于0.5则\(y = 1\)，如果小于0.5则\(y = 0\)，换一个角度来说，sigmoid中封装的线性回归函数在大于等于0的时候，\(y = 1\)，在小于0的时候，\(y = 0\)。

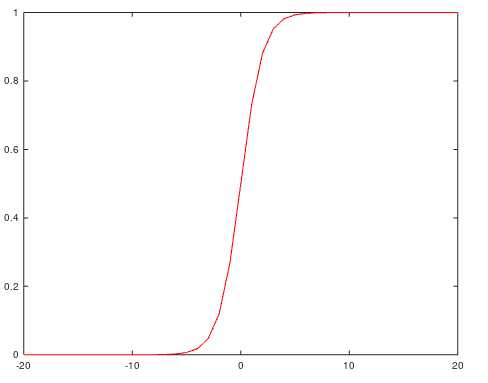
sigmoid function(logistic function)

• 定义
  • \({{1} \over {1 + e^{-x}}}\)
• 图像
  

根据学生的两次考试成绩来判断是否能够被大学录取

案例概要

• 第一列为第一次考试成绩列向量
• 第二列为第二次考试成绩列向量
• 第三列为是否被录取（0 or 1）

案例分析

• 定义假设函数\(h(x) = g(\theta^{T}x) = {{1} \over {1 + e^{-\theta^{T}x}}}\)。
• 数据变量
  • m: the number of training examples，样本的数量。
  • n: the number of features，特征的数量，这里不包括第0个特征，所以为2。
  • x的上标：样本的行数。
  • x的下标：表示第几个特征。

• 输入X，注意：这里的X已经添加上了默认的第0个特征，这个列向量中的值都为1
  \[ \begin{bmatrix} 1 & x^{1}_{1} & x^{1}_{2} \ 1 & x^{2}_{1} & x^{2}_{2} \ \vdots & \vdots & \vdots \ 1 & x^{m}_{1} & x^{m}_{2} \end{bmatrix} \]

• 目标函数（\(J(\theta)\)）
  • 与线性回归中一样\[J(\theta) = {{1} \over {2m}}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^{2} = {{1} \over {2m}}\sum_{i=1}^{m}({{1} \over {1 + e^{-\theta{x^{(i)}}}}} - y^{(i)})^{2}\]这里的\(\theta\)为列向量。
  • 思考，如何计算\(minimize_{\theta}J(\theta)\)
    • 在线性回归中我们使用梯度下降的方法可以很好的收敛，因为线性回归中的最小化方程是一个凸函数，没有局部最优点，只有一个全局最优点，但是在逻辑回归中，因为我们将线性回归函数封装到了sigmoid函数中，导致目标函数\(J(\theta)\)与\(\theta\)构成的函数图像是弯弯曲曲的，有多个局部最优点，导致了无法使用梯度下降的方法求出最优解。
    • 此时应该对目标函数进行等价替换（注意：等价替换值得是效果一样，但是数值可能不同）
      • 首先\[J(\theta) = {{1} \over {2m}}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^{2} = {{1} \over {m}}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^{2}\]
      • 接着定义Cost函数\[Cost(h_{\theta}({x^{(i)}}), y^{(i)}) = (h_{\theta}(x^{(i)}) - y^{(i)})^{2}\]，为什么？因为我们接下来要将\[(h_{\theta}(x^{(i)}) - y^{(i)})^{2}\]等价替换成一个分段函数，在机器学习的数学公式表示中，如果遇到一个分段函数，则在原来函数中使用一个新的逻辑函数（为什么说是抽象函数？因为在这里这个新的函数还没有函数的实体）将其替换掉，再对这个新的变量进行定义。
      • 其次将Cost函数等价替换为
        \[ Cost(h_{\theta}({x^{(i)}}), y^{(i)}) = \begin{cases} -log(h_{\theta}({x^{(i)}})) & if & y = 1 \ -log(1 - h_{\theta}({x^{(i)}})) & if & y = 0 \end{cases} \]
        上面的等价替换就是将返回概率值的假设函数\(h_{\theta}(x^{(i)})\)转为取log之后的结果。

      • 现在目标函数\(J(\theta)\)为
        \[ J(\theta) = {{1}\over{m}}\sum_{i=1}^{m}Cost(h_{\theta}({x^{(i)}}), y^{(i)}) \ Cost(h_{\theta}({x^{(i)}}), y^{(i)}) = \begin{cases} -log(h_{\theta}({x^{(i)}})) & if & y = 1 \ -log(1 - h_{\theta}({x^{(i)}})) & if & y = 0 \end{cases} \]

      • 通过数学方法可以将上面的两个式子合并为一个
        \[ J(\theta) = -{{1}\over{m}}[\sum_{i=0}^{m}y^{(i)}log(h_{\theta}({x^{(i)}})) + (1 - y^{(i)})log(1 - h_{\theta}({x^{(i)}}))] \]

  • 梯度下降

    • 梯度（也就是偏导）
      • \(grad = {{\partial}\over{\partial{\theta}}}J(\theta)\)
    • 梯度下降
      • \(\theta_{j} := \theta_{j}- \alpha{{\partial}\over{\theta_{j}}}J(\theta)\)，对所有的特征都进行梯度下降
      • 展开来就是和线性回归一样的式子\[\theta_{j} := \theta_{j}- \alpha{\sum_{i=1}^{m}(h_{\theta}}(x^{(i)}) - y^{(i)})x_{j}^{(i)}\]
    • 不断地更新参数即可

如果y的值为0, 1, 2, 3，如果使用拟合出来的函数进行预测

• 思路和对一个函数求偏导是一样，当我们讨论y=0的情况时，就将其他的1，2，3情况都归为一类，一次类推，我们可以得出y=0，1，2，3的概率，只要\(max(h(x^{(i)}))\)即可

逻辑回归实战

原文：https://www.cnblogs.com/megachen/p/9938519.html