Generalized Linear Model (GLM) 广义线性模型

这一段主要讲的是广义线性模型的定义和假设，为了看明白逻辑回归，大家要耐着性子看完。

1.The exponential family 指数分布族

因为广义线性模型是围绕指数分布族的，因此需要先介绍，用NG大神的话说就是，“虽然不是全部，但是我们见过的大多数分布都属于指数分布族，比如：Bernoulli伯努利分布、Gaussian高斯分布、multinomial多项分布、Poisson泊松分布、gamma分布、指数分布、Dirichlet分布……”服从指数分布族的条件是概率分布可以写成如下形式：

η 被称作natural parameter，它是指数分布族唯一的参数
T(y) 被称作sufficient statistic，很多情况下T(y)=y a(η) 被称作 log partition function
T函数、a函数、b函数共同确定一种分布
接下来看一下为什么说正态分布（高斯分布）属于指数分布族：
正态分布（正态分布有两个参数μ均值与σ标准差，在做线性回归的时候，我们关心的是均值而标准差不影响模型的学习与参数θ的选择，因此这里将σ设为1便于计算）

2.构成广义线性模型的三个假设

• p(y | x; θ) ∼ ExponentialFamily(η). 输出变量基于输入变量的条件概率分布服从指数分布族
• our goal is to predict the expected value of T(y) given x. 对于给定的输入变量x，学习的目标是预测T(y)的期望值，T(y)经常就是y
• The natural parameter η and the inputs x are related linearly: η = θT x. η和输入变量x的关联是线性的：η = θT x

这三个假设其实指明了如何从输入变量映射到输出变量与概率模型，举例来说：线性回归的条件概率分布为正态分布属于指数分布族（参考笔记一中线性回归的似然函数部分）；我们的目标是预测T(y)的期望，由上面的计算我们知道T(y)=y，而y的期望值也就是正态分布的参数μ；由上面的计算我们知道μ=η，而η=θT x。因此，线性回归是广义线性回归的一个特例，它的模型是：

指数分布族(Exponential family distributions)

指数族：

其中，
η被称作自然参数或正则参数(natural parameter/canonical parameter);
T(y)被称作充分统计量(sufficient statistic)，通常T(y)=y；
a(y)是log partition function，e−a(η)是一个规范化常数，使得分布p(y;η)的和为1。
对于给定的一组a,b,T，都会得到对应的指数分布族，而且改变参数η的取值会影响该指数族的分布。

伯努利分布(Bernoulli)的指数分布族

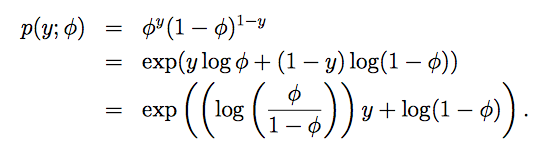
本例中η为标量，所以η=log(φ/(1−φ))

，即φ=1/(1+e−η)

。
这样我们就得到了一个logistic函数，也说明了伯努利分布的参数φ与自然参数η存在特定的关系。
指数分布族：

高斯分布(Gaussian)的指数分布族

在学习线性回归时，发现高斯分布的方差对最终结果并没有任何影响。所以为了简化问题，令σ2=1

。

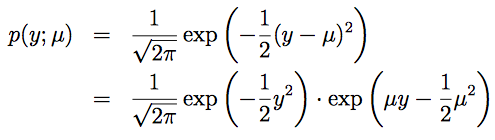
指数分布族：

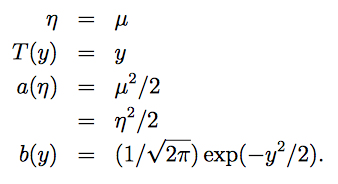
以下分布也都可以写成指数分布族的形式：
多项式分布(multinomial)
泊松分布(poisson)：用于计数的建模。
伽马分布(gamma)，指数分布(exponential):用于对正数建模，多用于间隔问题。
β分布，Dirichlet分布：用于对小数建模。

GLMs

广义线性模型(Generalized Linear Models)
构造GLMs来解决问题，我们首先需要了解三个设计假设。

1. y|x;θ∼ExponentialFamily(η)

• 。
• 我们的目标是通过给定x，来预测T(y)期望(E[T(y)|x]

)。由于通常T(y)=y，因此假设函数需要满足h(x)=E[y|x]

• (这个假设对logistic回归和线性回归都成立)。
• 自然函数η与输入特征x的关系是线性的，η=θTx

(如果自然参数是向量，ηi=θTix

3. )。

如果我们的问题需要满足这三个假设，那么我们就可以通过构造广义线性模型来解决。

最小二乘法

在线性回归的最小平方问题中，目标变量y(在GLM的术语中也称作响应变量(response variable))是连续的，给定x，y的条件分布符合高斯分布，均值为μ。套用前面GLM的推导，我们有μ=η。所以，我们可以得到线性回归的假设函数就是：

Logistic回归

在二元分类问题中，给定x，y服从伯努利分布，均值为?。同样利用前面的推导，可以得到logistic回归的假设函数就是：

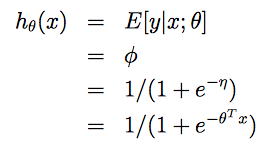
再介绍一些有关知识：
正则关联函数(canonical response function)：g(η)=E[T(y);η]

正则响应函数(canonical link function)：g−1

Softmax回归

多项式分布，多类别分类问题。
假设y∈{1,2,...,k}

，可以用一个k维的向量来表示分类结果，当y=i时，向量的第i个元素为1，其它均为0。这样表示是存在冗余的，因为如果我们知道了前k-1个元素，那么第k个其实就已经确定了，因此我们可以只用k-1维向量来表示。
设置参数：φ1,φ2,...,φk−1，φi=p(y=i;φ)。
由此可见：φk=1−∑k−1i=1φi。

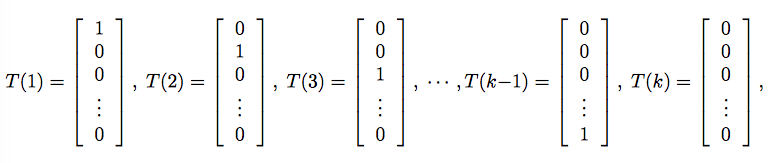
注意，这里就和前面的T(y)=y不同了，这里的T(y)是一个向量，所以用T(y)i

表示T(y)的第i个元素。在往后的推导过程中，会出现1{True}=1，1{False}=0的判别函数。所以T(y)与y的关系可以写成：

多项式分布的指数分布族：

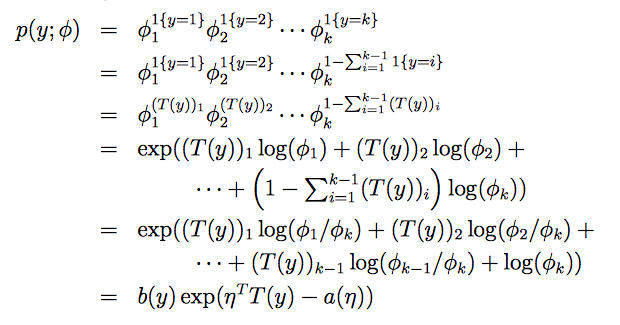
可以得到：

链接函数为ηi=logφiφk

,为了简化，令ηk=0，可得响应函数：

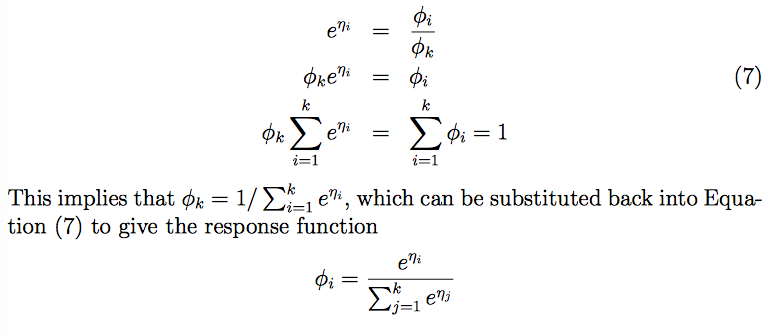
这个从η到φ’s的映射被称作softmax函数。
根据假设3，并且令θk=0，ηk=θTkx=0，得到softmax回归模型，它是logistic回归的推广。

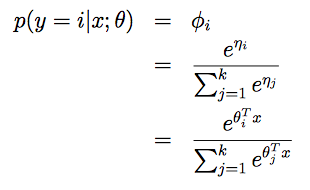
所以我们假设函数的输出为：

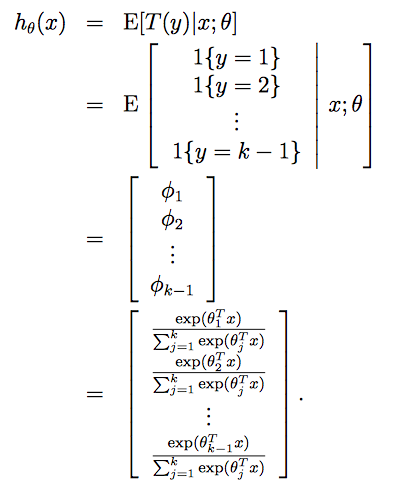
最后就是回归问题的参数的学习了，依然可以使用极大似然估计的方法来学习θ，似然函数为：

斯坦福CS229机器学习课程笔记 part3：Greneralized Linear Models (GLMs) 广义线性模型

原文：https://www.cnblogs.com/maxiaodoubao/p/9896279.html