原地址：http://blog.163.com/zpfzcjndx@126/blog/static/635456812013017115922938/
弧长法（Riks method）是目前结构非线性分析中数值计算最稳定、计算效率最高且最可靠的迭代控制方法之一，它有效地分析结构非线性前后屈曲及屈曲路径跟踪使其享誉"结构界"。大多数商业有限元软件(如ABAQUS、ANSYS等)也都将其纳入计算模块，作为一名工科生，机械式地"Step by Step"点击这些商业软件对话框的时候需"知其然，知其所以然"，否则必将"Rubbish in，Rubbish out"。
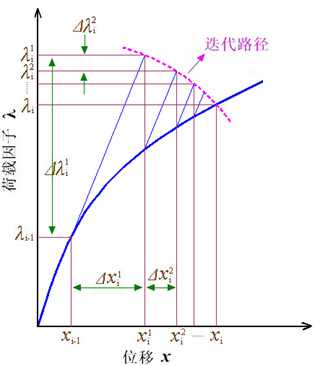
图1 弧长法迭代求解过程
图1 所示为弧长法的迭代求解过程，下标
表示第个荷载步，上标
表示第个荷载步下的第次迭代，显然，若荷载增量
，则迭代路径为一条平行于
轴的直线，即为著名的牛顿—拉夫逊法。
设第
个荷载步收敛于
，那么对于第个荷载步来说，需要进行次迭代才能达到新的收敛点
。外部参照力
，在ABAQUS需要用户以外荷载的形式输入，因此，作用在结构上的真实力大小为
。由于牛顿—拉夫逊法在迭代过程中，以荷载控制（或位移控制）时，荷载增量步
（或位移增量步）为常数，它无法越过极值点得到完整的荷载—位移曲线，事实上，也只有变化的荷载增量步才能使求解过程越过极值点。从图1中可以看出，弧长法的荷载增量步是变化的，可以自动控制荷载，但这又使原方程组增加了一个多余的未知量，因此需要额外补充一个控制方程，即：
（1）
该控制方程说明，其迭代路径是以上一个荷载步收敛点为圆心半径为
的圆弧，所以称为弧长法。通常用户需指定初始弧长半径
或固定的弧长半径
，当设定了初始弧长半径时，根据收敛速率，一般按式（2）计算，其中
为荷载步期望收敛迭代次数，一般取6, 
为上一荷载步的迭代次数，大于10时取10。
（2）
1. 当
时，根据上一个荷载步收敛结束时的构形，得到用于第个荷载步收敛计算的切线刚度矩阵
，即图1中的蓝色平行线的斜率。通过式（2）可得相应的切线位移。
（3）
（4）
（5）
很容易由式（5）求得，但不能确定其符号，而的符号决定了跟踪分析是向前还是返回，因此非常重要。很多学者提出了不同的确定方法，Murray j.Clarke（1993），A Study of Incremental-iterative Strategies for Non-linear Analysis这篇文章详细地介绍了这些方法。 在ABAQUS中，符号按下式（6）确定：
（6）
2. 当
时，为了简化
的求解过程，可以切平面法求解，即用垂直于切线的向量代替圆弧，即：
需要补充的关系式为：
最后需要说明的是，假若考虑材料塑性行为，则每个迭代步的切线刚度矩阵应以当前迭代步的构形为准，即图1中的蓝色切线不再平行。
原地址：http://blog.163.com/zpfzcjndx@126/blog/static/6354568120134228927334/
算例1. 如图1所示的平面杆系结构，顶点受到竖直向下的力P作用，用本程序（Riks method）进行计算，并将计算结果与精确解进行比较，如图2所示，通过对比可以说明本程序是正确的。
图1 计算简图
图2 跨中节点荷载—位移曲线对比
算例2：图3是经典的Lee‘s frame简图，一个在端部正交的铰接约束平面刚架，在距离正交点一定距离处有集中力F作用。之所以称其为经典算例是因为它的荷载位移曲线同时集中了跳跃(snap-through )和回弹(snap-back)现象，传统的求解策略根本无法对其进行荷载—位移路径跟踪，在此，弧长法展现了很大优势，图4是运用本程序得到刚架的变形动画，图5是加载点的荷载位移曲线，并将其与ABAQUS计算结果进行对比，通过对比表明该程序的是正确的。
图3 Lee‘s Frame 简图
图4 Lee‘s frame变形动画
图2 加载节点荷载—位移曲线对比
程序核心部分：
读取数据文件（节点、单元、约束、截面属性、参考力、控制弧长、最大控制参量）
while 控制参量（如位移、最大荷载因子） < 最大控制参量
计算当前切线刚度矩阵 K_Global
计算参考位移 X_Ref= 参考力\K_Global
计算初始荷载因子 lamda0=Arclength/sqrt(1+X_Ref‘*X_Ref);
判定初始荷载因子方向 +/- lamda0
更新节点坐标，更新外力
计算当前节点反力
计算节点不平衡力Val
while norm(Val)>1e-6
计算不平衡力产生的位移X_Val
计算荷载因子修正参数delta=X_Val‘*X_Ref/(1+X_Ref‘*X_Ref);
修正荷载因子lamda1=lamda0-delta;
更新初始荷载因子lamda0=lamda1;
更新节点坐标，更新外力
计算当前节点反力
计算节点不平衡力Val
end
end
原文：https://www.cnblogs.com/shoout/p/9734744.html