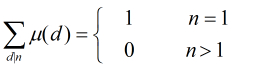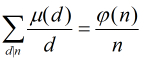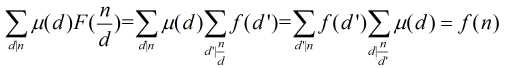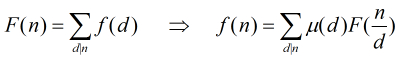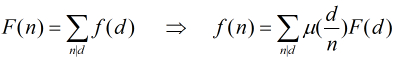题目描述
神犇YY虐完数论后给傻×kAc出了一题
给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对
kAc这种傻×必然不会了,于是向你来请教……
多组输入
输入输出格式
输入格式:
第一行一个整数T 表述数据组数
接下来T行,每行两个正整数,表示N, M
输出格式:
T行,每行一个整数表示第i组数据的结果
输入输出样例
说明
T = 10000
N, M <= 10000000
题目要求的就是∑ni=1∑mj=1[gcd(x,y)=prim]
化简出来Ans=∑T=1min(n,m)⌊nT⌋⌊mT⌋(∑t|T,t∈primeμ(⌊Tt⌋))
就是整除分块啦
#include<bits/stdc++.h> #define N 10000005 bool vis[N]; long long sum[N]; int prim[N]; int mu[N],g[N]; int cnt; void get_mu() { mu[1]=1; for(int i=2; i<N; i++) { if(!vis[i]) mu[i]=-1,prim[++cnt]=i; for(int j=1; j<=cnt&&prim[j]*i<N; j++) { vis[i*prim[j]]=1; if(i%prim[j]==0)break; else mu[prim[j]*i]=-mu[i]; } } for(int j=1; j<=cnt; j++)for(int i=1; i*prim[j]<N; i++)g[i*prim[j]]+=mu[i]; for(int i=1; i<N; i++)sum[i]=sum[i-1]+g[i]; } int n,m; int main() { get_mu(); int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&m); if(n>m)std::swap(n,m); long long ans=0; for(int l=1,r; l<=n; l=r+1) r=std::min(n/(n/l),m/(m/l)),ans+=1ll*(n/l)*(m/l)*(sum[r]-sum[l-1]); printf("%lld\n",ans); } return 0; }

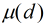 函数,它的定义如下:
函数,它的定义如下: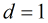 ,那么
,那么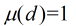
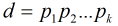 ,
,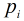 均为互异素数,那么
均为互异素数,那么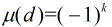
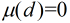
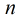 有
有