输入:
5
1 2 2
1 3 1
2 4 5
2 5 4
输出:
135
此题求图中两点之间的最长路径,我们可以从任意一点p开始dfs找到一点q,使得pq最长,然后以q为端
点,开始重复上一步的操作,求得最长路径sum,得路费ans=10*sum+(1+sum)*sum/2;
证明:假设最长路径为s--t,第一次dfs得到p-q;
(1)
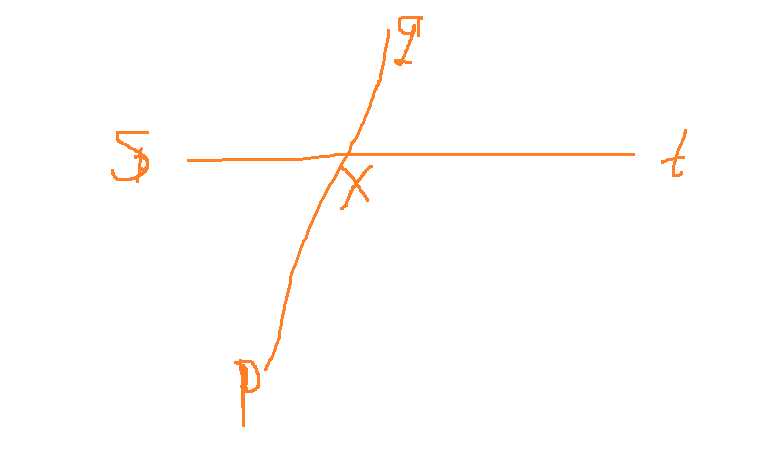
如果pq与st相交于x,因为px+xq>px+(st或者xt),sx+xt>sx+(xq或者xp),所以矛盾,所以q为最长路径的一个端点(s或者t)。
(2)
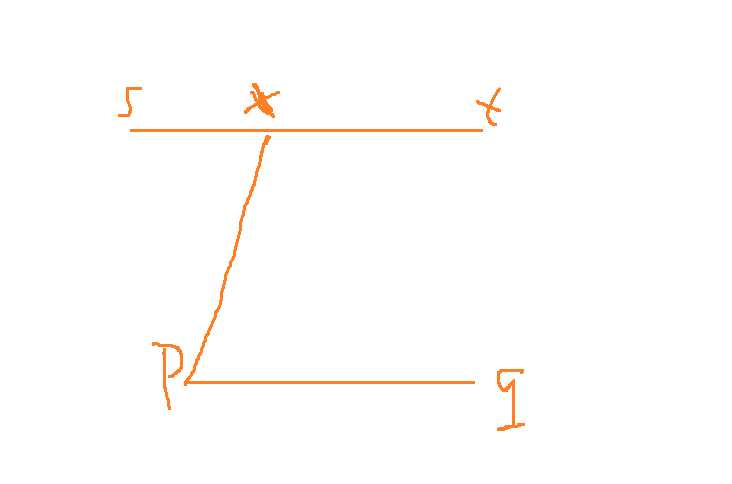
如果pq与st不相交,那么在st上任取一点x,显然pq>px+xt,可得pq+px>xt,又可得pq+px+xs=sq>xt+xs=st,与假设矛盾。
所以可得从任意一点dfs得到图中最长直径的一个端点。
代码如下:
1 #include <iostream> 2 #include <stdio.h> 3 #include <stdlib.h> 4 #include <string.h> 5 #include <algorithm> 6 #include <vector> 7 #include <math.h> 8 using namespace std; 9 #define N 74444 10 typedef long long ll; 11 vector<pair<int,ll> >g[N]; 12 int lie; 13 ll sum[N],S; 14 void dfs(int fa,int now) 15 { 16 int len=g[now].size(); 17 pair<int,long long>p; 18 for(int i=0;i<len;i++) 19 { 20 p=g[now][i]; 21 if(p.first!=fa) 22 { 23 sum[p.first]=sum[now]+p.second; 24 if(S<sum[p.first]){ 25 lie=p.first; 26 S=sum[p.first]; 27 } 28 dfs(now,p.first); 29 } 30 } 31 } 32 int main() 33 { 34 int n; 35 scanf("%d",&n); 36 for(int i=1;i<n;i++) 37 { 38 int x,y; 39 long long v; 40 scanf("%d%d%lld",&x,&y,&v); 41 g[x].push_back(make_pair(y,v)); 42 g[y].push_back(make_pair(x,v)); 43 } 44 S=0; 45 dfs(0,1); 46 S=0; 47 memset(sum,0,sizeof(sum)); 48 dfs(0,lie); 49 printf("%lld\n",S*10+(1+S)*S/2); 50 return 0; 51 }
原文:https://www.cnblogs.com/daimakuangmo/p/9606601.html