首先介绍一下莫比乌斯函数的形式
1. 当d=1d=1时,μ(d)=1 2. 当d=p1*p2*p3*…*pk且pi为互异素数时,μ(d)=(?1)^k。(说直白点,就是d分解质因数后,没有幂次大于平方的质因子,此时函数值根据分解的个数决定) 3. 只要当d含有任何质因子的幂次大于2,则函数值为0
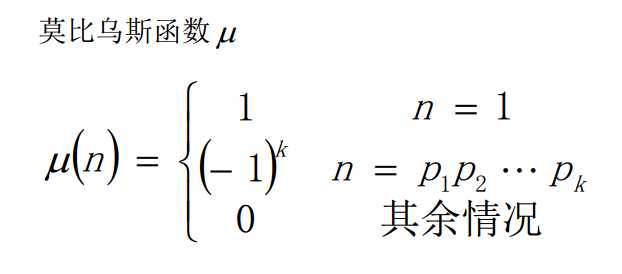
在线性筛(欧拉筛法)的基础之上稍加修改就可以得到筛莫比乌斯函数的,函数
1 #include<cstdio> 2 const int maxn=105; 3 int cnt; 4 bool vis[maxn]; 5 int mu[maxn],prim[maxn]; 6 void get_mu(int n) 7 { 8 mu[1]=1; 9 for(int i=2;i<=n;i++) 10 { 11 if(!vis[i]) {prim[++cnt]=i;mu[i]=-1;} 12 for(int j=1;j<=cnt&&prim[j]*i<=n;j++) 13 { 14 vis[prim[j]*i]=1; 15 if(i%prim[j]==0) break; 16 else mu[i*prim[j]]=-mu[i]; 17 } 18 } 19 } 20 int main() 21 { 22 get_mu(100); 23 for(int i=1;i<=100;i++) 24 printf("%d ",mu[i]); 25 return 0; 26 }
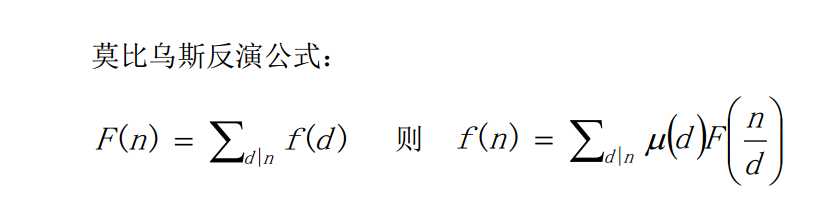
还有其变式形式:
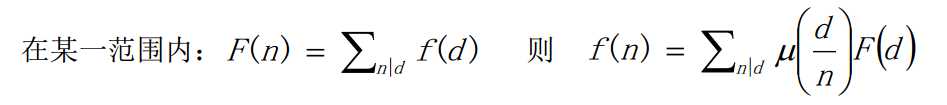
据说这种形式更加常用哦
BZOJ2301,它的题意是这样的,
对于给出的 n 个询问,每次求有多少个数对(x,y),满足 a≤x≤b, c≤y≤d,且 gcd(x,y) = k,
gcd(x,y)函数为 x 和 y 的最大公约数
设calc(n,m)表示在1<=x<=n,1<=y<=m,满足gcd(x,y)是k的(x,y)的对数
那么当限定区间在(a,b)和(c,d)的时候,可以根据容斥原理确定出来
原文:https://www.cnblogs.com/aininot260/p/9573650.html