| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 41143 | Accepted: 14068 |
Description

Input
Output
Sample Input
9 100 200 400 300 400 300 300 400 300 400 400 500 400 500 200 350 200 200 200
Sample Output
1628
Hint
Source
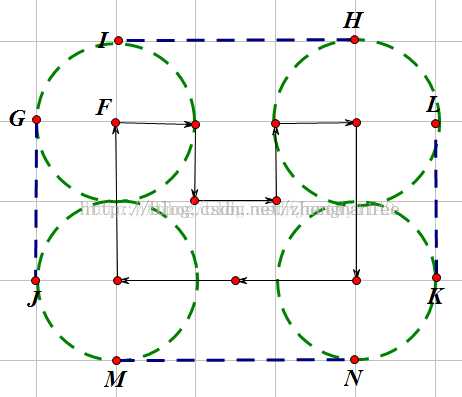
证明:
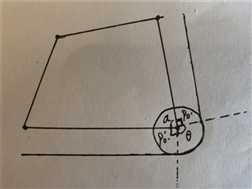
先从简单的例子看起:假设现在的凸包有四个顶点构成,可以就一个顶点来观察,我们可以看到此处的周角由四个部分组成:2个直角,一个凸包内角,一个圆弧对应的圆心角。
同理每个顶点都有类似的关系,同时周角固定为360度,而凸包内角和为(4-2)*180 ;
所以总的圆弧对应的圆心角 = 4个周角 - 4 * 2个直角 - 4个凸包内角 = 4 * 360 - 4 * 2 * 90 - (4-2)*180 = 1440-720-360 =360度。
现在推广到n个顶点的凸包:
则所有内角和 = 周角 * n - n * 2个直角 - (n-2)*180 = 360*n - n *180 - n*180 + 360 = 360度。
故对于任意的凸包,所有的圆弧对应的圆心角之和都为360度,它们构成一个完整的圆。
ac代码如下:
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
#define N 10005
const double PI = acos(-1.0);
int n,tot;//n为二维平面上点的个数,tot为凸包上点的个数
struct node {
int x,y;
}a[N],p[N]; //p[]用来储存凸包
double dis(node a1,node b1){ //两点间距离公式
return sqrt((a1.x-b1.x)*(a1.x-b1.x)+(a1.y-b1.y)*(a1.y-b1.y) + 0.00);
}
//叉积:返回结果为正说明p2在向量p0p1的左边(三点构成逆时针方向);
//为负则相反;为0则三点共线(叉积的性质很重要)
double multi(node p0,node p1,node p2){ //
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
//极角排序:极角排序是根据坐标系内每一个点与x轴所成的角,逆时针比较。按照角度从小到大的方式排序
int cmp(node p1,node p2){ //极角排序;
int x=multi(p1,p2,a[0]);
if(x>0||(x==0&&dis(p1,a[0])<dis(p2,a[0])))
return 1;
return 0;
}
void Graham(){ //求凸包
int k=0;
for(int i=0;i<n;i++) //找到最下最左的一个点
if(a[i].y<a[k].y||(a[i].y==a[k].y&&a[i].x<a[k].x))
k=i;
swap(a[0],a[k]); //将其设置为第一个点
sort(a+1,a+n,cmp);
tot=2,p[0]=a[0],p[1]=a[1]; //p[]模拟栈,用来储存凸包
for(int i=2;i<n;i++){
while(tot>1&&multi(p[tot-1],p[tot-2],a[i])>=0)
tot--; //右拐就回退
p[tot++]=a[i]; //左拐就放入
}
}
double getArea(){
struct node b[3];
b[0] = p[0], b[1] = p[1], b[2] = p[2];
double area = 0;
for(int i = 2; i < tot; i++){
area += multi(b[0], b[1], p[i]) / 2.0;
b[1] = p[i];
}
return area;
}
double getGirth(){
double rt = 0;
for(int i = 0; i < tot; i++){
rt += dis(p[i], p[(i+1)%tot]);
}
return rt;
}
int main(){
double L;
while(cin >> n >> L){
tot = 0;
for(int i = 0; i < n; i++){
cin >> a[i].x >> a[i].y;
}
Graham();
double res = getGirth();
res += 2*PI*L;
cout << int(res + 0.5) << endl;
}
return 0;
}
原文:https://www.cnblogs.com/zhumengdexiaobai/p/9530550.html