主要内容:
一.K-means算法简介
二.算法过程
三.随机初始化
四.K的选择
一.K-means算法简介
1.K-means算法是一种无监督学习算法。所谓无监督式学习,就是输入样本中只有x,没有y,即只有特征,而没有标签,通过这些特征对数据进行整合等操作。而更细化一点地说,K-means算法属于聚类算法。所谓聚类算法,就是根据特征上的相似性,把数据聚集在一起,或者说分成几类。
2.K-means算法作为聚类算法的一种,其工作自然也是“将数据分成几类”,其基本思路是:
1) 首先选择好将数据分成k类,然后随机初始化k个点作为中心点。
2) 对于每一个数据点,选取与之距离最近的中心点作为自己的类别。
3) 当所有数据点都归类完毕后,调整中心点:把中心点重新设置为该类别中所有数据点的中心位置,每一轴都设置为平均值。(所以称为means)
4) 重复以上2)~3)步骤直至数据点的类别不再发生变化。
3.K-means算法从感性上去理解,就是把一堆靠得近的点归到同一个类别中。
二.算法过程
1.一些变量的约定:μ(i)表示第i个中心点,c(i)表示第i个数据点归到哪个中心点。
2.K-means算法的本质就是:移动中心点,使其渐渐地靠近数据的“中心”,即最小化数据点与中心点的距离。即:

3.算法流程:

三.随机初始化
由于初始化的中心点对于最后的分类结果影响很大,因而很容易出现:当初始化的中心点不同时,其结果可能千差万别:
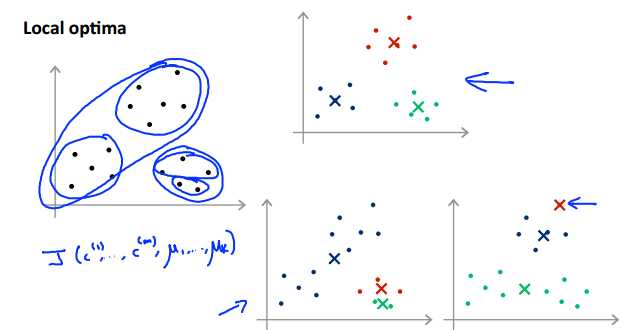
因此,为了分类结果更加合理,我们可以多次初始化中心点,即多次运行K-means算法,然后取其中J(c1,c2……,μ1,μ2……)最小的分类结果。

四.K的选择
最后一个问题:既然是K-means,那么这个k应该取多大呢?
一.Elbow method:
假设随着k的增大,cost function j的大小呈现以下的形状:
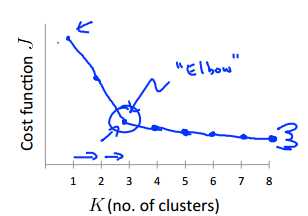
可以看到,当k=3时,J已经很小了,且再增大k也不能大大地减小J。说明此时k选取3比较合适。
但是,这种“手肘”情况并不常见,更一般的情况是:
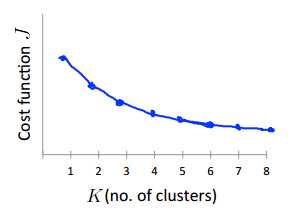
此时根本看不出哪里才是“手肘”,所以对此的策略是:实践调研,按实际需求的而定。
原文:https://www.cnblogs.com/DOLFAMINGO/p/9360120.html